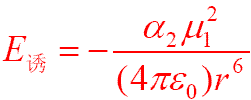分子間作用力，又稱范德華力（van der Waals force）。分子間作用力（范德華力）有三個來源：①極性分子的永久偶極矩之間的相互作用。②一個極性分子使另一個分子極化，產生誘導偶極矩並相互吸引。③分子中電子的運動產生瞬時偶極矩，它使鄰近分子瞬時極化，後者又反過來增強原來分子的瞬時偶極矩；這種相互耦合產生靜電吸引作用，這三種力的貢獻不同，通常第三種作用的貢獻最大。
分子間作用力是只存在於分子(molecule)與分子之間或惰性氣體(noble gas)原子(atom)間的作用力，又稱范德華力(van der waals)，具有加和性，屬於次級鍵。
氫鍵(hydrogen bond)、弱范德華力、疏水作用力、芳環堆積作用、鹵鍵都屬於次級鍵（又稱分子間弱相互作用）。
基本介紹
氫鍵,作用力分類,色散力,誘導力,取向力,三種力的關係,相關概念辨析,性質,相關實驗,
氫鍵
氫鍵屬不屬於分子間作用力，取決於對“分子間作用力”的定義。按照廣義范德華力定義[引力常數項可將各種極化能（偶極(dipole)、誘導(induced)和氫鍵能）歸併為一項來計算]，氫鍵屬於分子間作用力。按照傳統定義：分子間作用力定義為：“分子的永久偶極(permanent dipole)和瞬間偶極(instantaneous dipole)引起的弱靜電相互作用”那么氫鍵不屬於（因為氫鍵至少包含四種相互作用，只有三種與分子間作用力有交集，但還存在最高被占用軌道與另一分子最低空餘軌道發生軌道重疊）。
氫鍵既可以存在於分子內也可以存在於分子間。其次，氫鍵與分子間作用力的量子力學計算方法也是不一樣的。另外，氫鍵具有較高的選擇性，不嚴格的飽和性和方向性；而分子間作用力不具有。在“摺疊體化學”中，多氫鍵具有協同作用，誘導線性分子螺旋，而分子間作用力不具有協同效應。超強氫鍵具有類似共價鍵(covalent bond)本質，在學術上有爭議，必須和分子間作用力加以區分。
作用力分類
定義：范德華力（又稱分子作用力）產生於分子或原子之間的靜電相互作用。其能量計算的經驗方程為:U =B/r- A/r (對於2 個碳原子間,其參數值為B =11.5 ×10 kJ·nm/mol ；A=5.96 × 10 kJ·nm/mol；不同原子間A、B 有不同取值）當兩原子彼此緊密靠近電子云相互重疊時，發生強烈排斥，排斥力與距離12 次方成反比。低點是范德華力維持的距離作用力最大，稱范德華半徑。分子引力與距離6次方成反比，分子斥力與距離12次方成反比。
色散力
誘導力
誘導力（induction force）在極性分子和非極性分子之間以及極性分子和極性分子之間都存在誘導力。由於極性分子偶極所產生的電場對非極性分子發生影響，使非極性分子電子云變形(即電子云被吸向極性分子偶極的正電的一極)，結果使非極性分子的電子云與原子核發生相對位移，本來非極性分子中的正、負電荷重心是重合的，相對位移後就不再重合，使非極性分子產生了偶極。這種電荷重心的相對位移叫做“變形”，因變形而產生的偶極，叫做誘導偶極，以區別於極性分子中原有的固有偶極。誘導偶極和固有偶極就相互吸引，這種由於誘導偶極而產生的作用力，叫做誘導力。在極性分子和極性分子之間，除了取向力外，由於極性分子的相互影響，每個分子也會發生變形，產生誘導偶極。其結果使分子的偶極距增大，既具有取向力又具有誘導力。在陽離子和陰離子之間也會出現誘導力。
括弧里取平方
誘導力與極性分子偶極矩的平方成正比。誘導力與被誘導分子的變形性成正比，通常分子中各原子核的外層電子殼越大（含重原子越多）它在外來靜電力作用下越容易變形。相互作用隨著1/r 而變化，誘導力與溫度無關。其公式：α為極化率。
取向力
取向力（orientation force 也稱dipole-dipole force）取向力發生在極性分子與極性分子之間。由於極性分子的電性分布不均勻，一端帶正電，一端帶負電，形成偶極。因此，當兩個極性分子相互接近時，由於它們偶極的同極相斥，異極相吸，兩個分子必將發生相對轉動。這種偶極子的互相轉動，就使偶極子的相反的極相對，叫做“取向”。這時由於相反的極相距較近，同極相距較遠，結果引力大於斥力，兩個分子靠近，當接近到一定距離之後，斥力與引力達到相對平衡。這種由於極性分子的取向而產生的分子間的作用力，叫做取向力。取向力與分子的偶極矩平方成正比，即分子的極性越大，取向力越大。取向力與絕對溫度成反比，溫度越高，取向力就越弱關相互作用隨著1/r而變化。其公式為：μ1，μ2為兩個分子的偶極矩；r為分子質心間的距離，k為Boltzmann 常數，T為熱力學溫度，負值表示能量降低。
三種力的關係
極性分子與極性分子之間，取向力、誘導力、色散力都存在；極性分子與非極性分子之間，則存在誘導力和色散力；非極性分子與非極性分子之間，則只存在色散力。這三種類型的力的比例大小，決定於相互作用分子的極性和變形性。極性越大，取向力的作用越重要；變形性越大，色散力就越重要；誘導力則與這兩種因素都有關。但對大多數分子來說，色散力是主要的。實驗證明，對大多數分子來說，色散力是主要的；只有偶極矩很大的分子(如水)，取向力才是主要的；而誘導力通常是很小的。極化率α反映分子中的電子云是否容易變形。雖然范德華力只有0.4—4.0kJ/mol，但是在大量大分子間的相互作用則會變得十分穩固。比如C—H 在苯中范德華力有7 kJ/mol，而在溶菌酶和糖結合底物范德華力卻有60kJ/mol，范德華力具有加和性。
所以真正關鍵字是“距離”，我們可以把分子作用力、離子鍵放在一起考慮。
作用類型 | 能量和距離關係 |
荷電基團靜電作用 | 1/r |
離子—偶極子 | 1/r |
離子—誘導偶極 | 1/r |
偶極子—偶極子 | 1/r取向力化學 |
偶極子—誘導偶極子 | 1/r誘導力 |
誘導偶極子-誘導偶極子 | 1/r色散力 |
非鍵排斥 | 1/r—1/r |
在生物學中重點是了解有機分子的離子相互作用。有機分子形成的離子，電負性差異沒有那么大，相互作用不像這些典型的離子化合物離子鍵這樣大，所以就稱為離子相互作用；但他們的共同點都是靠靜電引力做形成的。
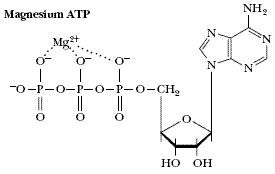
ATP 和鎂離子相互作用
NaCl、CsCl、CaF2、立方ZnS、六方ZnS、金紅石TiO2 這六種典型化合物的晶體構型其離子鍵能量是和距離一次方成反比，Mg和ATP 的相互作用，胺基酸兩性離子間的相互作用。離子—偶極子是隨距離二次方而減小，離子—誘導偶極子是隨距離4次方而減小。所以生物分子中的離子相互作用（也稱鹽鍵）是弱相互作用，是隨1/r—1/r而減小。
相關概念辨析
詞條被修改62次在於，不同筆者對氫鍵與分子間作用力從屬關係的爭論。
傳統定義，將分子間作用力定義為：“分子的永久偶極和瞬間偶極引起的弱靜電相互作用”。隨著研究的深入，發現了許多用現有分子間作用力的作用機理無法說明的現象。比如鹵鍵，有機汞鹵化物時觀察到分子內鹵素原子與汞原子之間存在長距離強的共價相互作用力，從而引入二級價鍵力(secondary valence forces)的概念。
氫鍵是否屬於分子間作用力取決於對”分子間作用力“的定義。如果“分子間作用力”繼續被狹義指代“分子的永久偶極和瞬間偶極引起的弱靜電相互作用”。這樣氫鍵與分子間作用力性質也不完全相同，量子力學計算方法也不完全同……，更像並列關係，氫鍵就不屬於分子間作用力。而我們目前國內普通化學教材、百科大辭典等，就是這個定義，就是狹義指代范德華力。
如果”分子作用力“定義指代一切分子的相互作用（這個定義也包括了長程和短程的相互作用），那么氫鍵也屬於分子間作用力，不僅氫鍵屬於，離子鍵力也屬於分子間作用力。《高分子界面科學》一書，張開教授認為引力常數項可將各種極化能（偶極、誘導和氫鍵能）歸併為一項來計算從這一角度出發，范德華力偶極矩相互作用係數可擴大範圍寫成靜電相互作用係數。這樣得到了關於靜電力的廣義范德華力。這樣分子間相互作用的分類一些文獻也有報導。《流體的熱物理化學性質—對應態原理及其套用》作者項紅衛教授認為分子作用勢能的三個類型統稱范德華力，包括定向力、誘導力和色散力，定向力來源於偶極矩產生的引力包括電荷、偶極和四級矩其相互作用由玻爾茲曼權重因子按1/kT冪指數展開可得到平均勢能函式。電荷、偶極和四級矩這些類型的相互作用十分相似均可認為服從Berthelot規律。由於色散力不會產生誘導作用，實際誘導相互作用按靜電力比例修正。
張季爽和申成對於HF量子計算表明，氫鍵的形成至少四種不同類型的相互作用，1.HF偶極矩的取向力；2.HF分子最高被占用軌道與另一分子最低空餘軌道發生軌道重疊和電荷轉移作用，即類共價鍵。3.分子間電子云的排斥作用。4.分子間的誘導偶極作用，非常微弱。氫鍵的本質也是靜電相互作用，主要是偶極作用能和靜電作用能近似可以用廣義范德華力計算式計算，氫鍵作用是氫鍵力的幾何平均值服從Berthelot規律。
由此來看，氫鍵包含分子間作用力“集合所構成的”元素，兩個集合無交集。但是氫鍵還具有它所不具有的特徵軌道重疊與電荷轉移。
超強氫鍵具有類似共價鍵本質，在學術上有爭議，必須和分子間作用力加以區分。
另外，由於存在爭議，其從屬概念的辨析取決於對”分子間作用“的基本定義。而加州大學伯克利分校的John M. Prausnitz指出：”我們對分子間作用力認識遠遠不夠，目前只局限於簡單理想情況“。 筆者認為因此在基礎教育，比如中學教育，不必嚴格區分從屬關係，重點在於了解性質。無論說氫鍵屬於或不屬於分子間作用力都不算錯誤。要將分子間作用力和氫鍵概念的辨析從屬關係的考試題可以從考試中剔除（考誰屬於誰是沒有意義的），可以休矣！學生更重要的在於了解，氫鍵的特性以及幾何平均關係、不嚴格飽和性和方向性、熔沸點、溶解度影響、穩定性以及π氫鍵等等。因為我們對分子間作用力認識遠遠不夠……
性質
組成和結構相似的物質，相對分子質量越大，范德華力越大，克服分子間引力使物質熔化和汽化就需要更多的能量，熔、沸點越高.但存在氫鍵時分子晶體的熔沸點往往反常地高。氣體分子之間的距離較大，故分子間的相互作用較小;液體和固體的存在，正是分子間有互相吸引作用的證明;而液體、固體的難於壓縮，又證明了分子間在近距離時表現出的排斥作用。
相關實驗
法國的科學家2013年首次對兩個原子之間的范德華力進行了直接的測量，所用實驗方法可以用來建立量子邏輯門，或者用來進行凝聚態系統的量子模擬。
原子偶極：首次直接測量原子間的范德華力
原子偶極：科學家首次直接測量原子間的范德華力
（圖片來源：iStockphoto/Nicemonkey）
原子間、分子間和物體表面間的范德華力以各種不同方式出現在日常生活中。例如，蜘蛛和壁虎就是依靠范德華力才能沿著平滑的牆壁向上爬，我們體內的蛋白質也是因為范德華力的存在才會摺疊成複雜的形狀。
范德華力是以荷蘭科學家約翰尼斯·迪德里克·范·德·瓦耳斯的名字命名的，他在1873年第一次提出了范德華力這個概念用以解釋氣體的行為。這種力非常微弱，只有當原子或者分子十分靠近的時候才有意義。原子電子云的漲落使得原子具有瞬時電偶極矩，從而誘導附近的原子產生電偶極矩，結果會產生相互吸引的偶極間相互作用。
間接測量
對原子間范德華力的間接測量已有非常多的研究成果，例如分析巨觀物體間的淨力來獲得經驗值，或者利用光譜學來分析雙原子分子中兩個原子間的長程作用力。但在這之前一直缺乏直接測量范德華力的相關研究。
這項最新的研究是由帕萊佐的查爾斯·法布里實驗室（Laboratoire Charles Fabry， LCF）和里爾大學（University of Lille）的研究人員共同完成的。“我們所做的是，直接測量兩個位於可控距離內的獨立原子間的范德華力，原子間的距離由實驗人員設定。據我們所知這是首次實現直接測量，”LCF團隊成員蒂埃里·拉哈耶（Thierry Lahaye）說。
在測量原子間作用力時，控制兩個普通原子之間的距離是極其困難的，因為相關的距離非常小。研究團隊利用里德伯原子來解決這個問題，它們比普通原子大很多。里德伯原子中有一個電子處於高激發態，這意味著它們有一個很大的瞬時電偶極矩，因此即使處於相對較遠的距離，也會存在較大的范德華力。它們同時還有某些獨特的性質，使得它們在實驗室中可以被精確控制。
原子對錯
實驗首先利用兩束高度聚焦的雷射束分別捕獲兩個銣原子，並將原子分隔開幾微米的距離。然後將一束特定波長的雷射束照射在原子上，使得體系在基態和一個或兩個里德伯原子之間振盪。研究團隊發現，當條件合適時，體系將在基態和一對里德伯原子之間振盪，此時兩個原子分別在兩束雷射的焦點上。通過測量這些振盪，研究人員計算出了兩個里德伯原子之間的范德華力。
研究人員通過調整捕獲雷射束，可以將里德伯原子靠近或拉遠。當研究人員改變原子之間的距離R時，作用力表現出與R的6次方呈反比的變化規律——這一結果和預期的范德華力完全一樣。
除了測量范德華力，研究團隊還發現兩個相互作用的里德伯原子的量子態演化是完全相干的。LFC團隊成員安托萬·布拉維斯（Antoine Browaeys）稱，這是“在原子物理中從未見到過的”。
與量子邏輯相似
兩個相互作用原子的相干演化和工作於兩個量子比特上的量子邏輯門是完全一樣的。布拉維斯認為，這說明通過范德華力進行相互作用的兩個原子是創建高保真量子門的理想系統，“這一結果讓我們向量子計算機又進了一步。”他說。
事實上，研究人員認為他們實驗的長遠意義並不在於測量范德華力本身，而是實現了對里德伯原子的精確控制。 “這使得我們能夠設計小的量子系統，並逐漸增加量子系統的尺寸，有希望從兩個里德伯原子逐漸增加到幾十個，而我們可以完全控制原子間的相互作用。”拉哈耶解釋道。
這樣的量子系統有望套用於量子信息處理或者凝聚態體系的量子模擬（例如量子磁體）等工作中。
並未參與此次研究的馬里蘭大學聯合量子研究所的史蒂文·羅爾斯頓（Steven Rolston）將這一成果稱作是重要的里程碑，他認為這將有助於量子信息設備的研發與製造，因為它證明了原子量子比特間的范德華力表現得與預期相同。
本研究發表於《物理評論快報》（Physical Review Letters）。
本文作者 卡蒂亞·摩斯科維奇是一位英國科學作家。
（翻譯：沈添懌）
