基本介紹
測量史
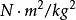
測定
 引力常量測定
引力常量測定
引力常數一般指本詞條
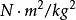
 引力常量測定
引力常量測定引力常量,是物理學術語,目前公認的結果是卡文迪許測定的G值為6.754×10-11N·m²/kg²,目前最新的推薦的標準為G=6.67408×10-11N·m²/kg²,通常...
地心引力常數GM是地球的基本特徵參數之一,單位為m3/s2。它是研究地球物理性質、地球重力場、地球動力形狀的重要參量;同時它在地球重力場範圍內及深空領域研究空間...
基本物理常數(fundamental constants of physics)是物理領域的一些普適常數。這些常數的準確數值,由於從理論上說與測量地點、測量時間及所用的測量儀器及材料均無關聯...
研究物質間的一種相互作用──引力作用的理論。在今天人們所知道的物質的四種基本相互作用中,引力作用為最弱。四種相互作用按作用強度比例順序是:強相互作用(1),...
天文常數之一。為引力常數與太陽質量的乘積。...... 中文名稱:日心引力常數;英文名稱:heliocentricgravitationalconstant;定義1:天文常數之一。為引力常數與太陽質量的...
常用物理基本常數表是一個表格。...... 引力常數 G0 阿伏加德羅 NA 目錄 1 定義 2 內容 常用物理基本常數表定義 編輯 常用物理基本常數表是一個表格。常用...
測得迄今最高精度的引力常數G值,2018年度中國科學十大進展之一。...... 2019年2月27日,測得迄今最高精度的引力常數G值入選中國科學十大進展。 [1] ...
引力勢又稱引力位(Gravitational potential),是一個有質量的物體所產生的標量場。...... 令某一點距其為r,此物體質量為M,引力位可表示成P=GM/r,其中G是引力...
引力(英語:Gravitation、Gravity),是指具有質量的物體之間加速靠近的趨勢,其來源於物體自身質量對於時空的彎曲,而不是源於重力場間的相互拉扯。 因此,引力並不是我們...
引力是質量的固有本質之一。每一個物體必然與另一個物體互相吸引。儘管引力的本質還有待於確定,但人們早已覺察到了它的存在和作用。接近地球的物體,無一例外地被...
萬有引力常數是一個實驗物理常數,用於計算兩個物體間的引力大小。通常出現在牛頓萬有引力方程和愛因斯坦廣義相對論中。一般用大寫G表示。萬有引力常量G的準確值計算...
引力場是描述物體延伸到空間中對另一物體產生吸引效應的理論模型。現代觀點認為引力場是物質在空間中產生的空間彎曲效應,物體在該彎曲空間內運動時表現出在直角空間中...
在物理學的基本常數中,有些是通過實驗觀測發現的,如真空中的光速c 、基本電荷e、磁常數(真空中的磁導率)μ0 、電常數(真空中的率)ε0 等.也有一些是在建立...
在自然科學中,為了描述自然規律,需要運用各種常數。在這些常數中,一類是有量綱的常數,例如,光速C,普朗克常數h,電子電荷e,質子質量mp,電子質量me,牛頓引力常數G,...
萬有引力定律是艾薩克·牛頓在1687年於《自然哲學的數學原理》上發表的。牛頓的普適萬有引力定律表示如下:任意兩個質點通過連心線方向上的力相互吸引。該引力的的...
引力場方程是指描述引力場的時空幾何量,作為引力場源的物質能量動量張量的方程。這個方程反映了愛因斯坦的馬赫原理的思想。1905年愛因斯坦發表狹義相對論後,他開始著眼...
哈勃常數的值通常經由遙遠星系的紅移來測量,這就是用與哈勃定律不同的方法測量同一星系的距離。...
假設地球質量是M,質點質量是m,質點所在緯度是θ,海拔高度h,此處的地球半徑是R,地球自轉的角速度是ω,萬有引力常數是G,質點和地球自轉軸之間的距離是r,那么顯然...
到了1690年左右,英國人牛頓以“萬有引力”概念解開行星軌道之謎,並且將克卜勒第三行星定律改進成 ,G是萬有引力常數,M是太陽質量,m是行星質量,P是公轉周期。 [...
