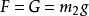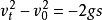重力加速度(物理名詞)

重力加速度（Gravitational acceleration）是一個物體受重力作用的情況下所具 有的加速度。也叫自由落體加速度，用g表示。方向豎直向下，其大小由多種方法可測定。

通常指地面附近物體受地球引力作用在真空中下落的加速度，記為g。為了便於計算，其近似標準值通常取為980厘米/秒的二次方或9.8米/秒的二次方。在月球、其他行星或星體表面附近物體的下落加速度，則分別稱月球重力加速度、某行星或星體重力加速度。

基本介紹

• 中文名：重力加速度
• 外文名：Gravitational acceleration
• 別稱：自由落體加速度
• 表達式：g=G*M/(r^2)
• 提出者：伽利略測定
• 套用學科：物理學
• 適用領域範圍：物理學
• 方向：豎直向下
• 符號：g
• 基本單位：m/s^2
• 常取值：9.8m/s^2或10m/s^2

基礎知識

定義

重力加速度（Gravitational acceleration）是一個物體受重力作用的情況下所具有的加速度。 假設一個質量為m的質點與一質量為M的均勻球體的球心距離為r時，質量所受的重力大小約等於兩物體間的萬有引力，為：

其中G為引力常數。 根據牛頓第二定律

F=ma=mg

可得重力加速度

三要素

大小：與位置有關；（G=mg) （其中g=9.80665 m/s^2，為標準重力加速度）

方向：豎直向下；

作用點：重心

證明

自由落體運動時，a=g。

證明： （ 為慣性質量， 為引力質量，經力學單位制統一後，兩者數值上相等）

因為

所以

所以a=g

自由落體

⒈初速度

⒉末速度V=gt

⒊下落高度 （從 位置向下計算）

⒋推論:

註：⑴自由落體運動是初速度為零加速度為g的勻加速直線運動，遵循勻變速直線運動規律；

⑵a=g=9.8m/ ≈10m/ （重力加速度在赤道附近較小，在高山處比平地小，方向豎直向下）。

⑶豎直上拋運動

⒈位移

⒉末速度 =gt （g=9.8m/ ≈10m/ ）

⒊有用推論

⒋上升最大高度 （拋出點算起）

⒌往返時間 （從拋出落回原位置的時間）

註：⑴全過程處理：是勻減速直線運動，以向上為正方向，加速度取負值；

⑵分段處理：向上為勻減速直線運動，向下為自由落體運動，具有對稱性；

⑶上升與下落過程具有對稱性，如在同點速度等值反向等。△s=

性質

重力加速度g的方向總是豎直向下的。在同一地區的同一高度，任何物體的重力加速度都是相同的。重力加速度的數值隨海拔高度增大而減小。當物體距地面高度遠遠小於地球半徑時，g變化不大。而離地面高度較大時，重力加速度g數值顯著減小，此時不能認為g為常數。

距離地面同一高度的重力加速度，也會隨著緯度的升高而變大。由於重力是萬有引力的一個分力，萬有引力的另一個分力提供了物體繞地軸作圓周運動所需要的向心力。物體所處的地理位置緯度越高，圓周運動軌道半徑越小，需要的向心力也越小，重力將隨之增大，重力加速度也變大。地理南北兩極處的圓周運動軌道半徑為0，需要的向心力也為0，重力等於萬有引力，此時的重力加速度也達到最大。

通常指地面附近物體受地球引力作用在真空中下落的加速度，記為g。為了便於計算，其近似標準值通常取為980厘米/秒^2或9.8米/秒^2。在月球、其他行星或星體表面附近物體的下落加速度，則分別稱月球重力加速度、某行星或星體重力加速度。

在近代一些科學技術問題中，需考慮地球自轉的影響。更精確地說，物體的下落加速度g是由地心引力F（見萬有引力）和地球自轉引起的離心力Q（見相對運動）的合力W產生的（圖1）。Q的大小為mω(RE+H）cosδ,m為物體的質量；ω為地球自轉的角速度；RE為地球半徑；H為物體離地面的高度；δ為物體所在的地球緯度。這個合力即實際見到的重力G=mg。地球重力加速度是垂直於大地水準面的。在海平面上g隨緯度δ變化的公式（1967年國際重力公式）為：

g=978.03185（1+0.005278895*sinδ^2+0.00023462*sinδ^4）厘米/秒。

在高度為H的重力加速度g（1930年國際重力公式）同H和δ有關，即

g =978.049（1+0.005288*sinδ^2-0.000006*sin2δ^2)- 0.03086*H 厘米/秒，

式中H為以千米為單位的數值。

最早測定重力加速度的是伽利略。約在1590年，他利用斜面將g的測定改為測定微小加速度a=gsinθ，θ是斜面的傾角。測量重力加速度的另一方式是阿脫伍德機。1784年，G.阿脫伍德將質量同為Μ的重塊用繩連線後，放在光滑的輕質滑車上，再在一個重塊上附加一重量小得多的重塊m（圖2）。這時，重力拖動大質量物塊，使其產生一微小加速度，測得a後，即可算出g。後人又用擺和2Μ+m各種優良的重力加速度計測定g。

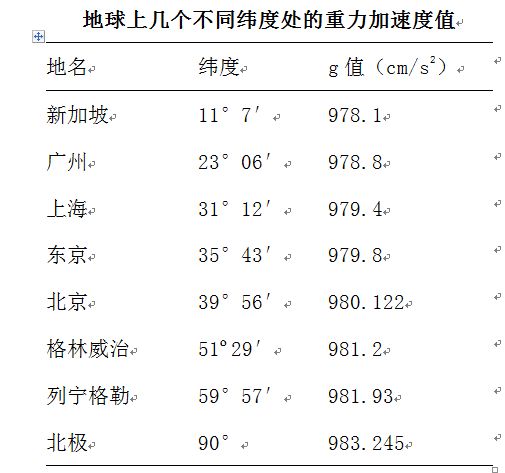
地球上幾個不同緯度處的g值見下表；從中可以看出g值隨緯度的變化情況：

由於地球有自轉，所以略微呈橢球形，在一般情況下，重力加速度的方向不通過地心。重力加速度的測定，對物理學、地球物理學、重力探礦、空間科學等都具有重要意義

概念延伸

地球表面

在地球表面附近，一質點的自由落體加速度g與它的重力加速度a稍微不同，一個質點的重量mg與它所受的重力（萬有引力和慣性力的共同作用叫重力）也不同，原因是地球會自轉。若考慮地球自轉，則：

(測量到的重量mg)=(萬有引力)-(質量m×向心加速度(w^2)*R)

可以得到：

(自由落體加速度g)=(萬有引力)-(向心加速度(w^2)*R)

注意以上式子中的減法為矢量相減。自由落體加速度實際上是小於重力加速度的，方向也略有區別，在赤道上則相差最多，但由於地球的半徑與自轉周期的關係，兩者大約只相差0.034m(s^2)，因此在日常使用的計算上，重量與重力之間的差異通常是可忽略的。

地表附近的所有物體下降的加速度都介於9.78和9.83m/(s^2);之間，差別是取決於緯度等因素(赤道最少，南北極最大)，標準重力加速度是9.80665 m/s^2;（為方便計算，一般使用9.81 m/(s^2);9.8 m/(s^2);或10 m(s^2);）。

常用數值

由於g隨經度變化不大，因此國際上將在緯度45°的海平面精確測得物體的重力加速度g=9.80665米/秒^2;作為重力加速度的標準值。在解決地球表面附近的問題中，通常將g作為常數，在一般計算中可以取g=9.80米/秒^2；。理論分析及精確實驗都表明，隨緯度的提高，重力加速度g的數值略有增大，如赤道附近g=9.780米/秒^2，

廣州g=9.788米/秒^2。

武漢g=9.794米/秒^2。

上海g=9.794米/秒^2。

東京g=9.798米/秒^2。

北京g=9.801米/秒^2。

紐約g=9.803米/秒^2。

莫斯科g=9.816米/秒^2。

北極地區g=9.832米/秒^2。

各緯度海平面的重力加速度（m/s2）

緯度	重力加速度	緯度	重力加速度
0	9.78030	30	9.79321
10	9.78186	40	9.80166
20	9.78634	50	9.81066
60	9.81914	80	9.83058
70	9.82606	90	9.83218

不同高度的重力加速度 (m/s^2）

海拔 (km)	緯度（度）
	0	10	20	30	40	50	60	70	80	90
0	9.780	9.782	9.786	9.793	9.802	9.811	9.819	9.826	9.831	9.832
4	9.768	9.770	9.774	9.781	9.789	9.798	9.807	9.814	9.818	9.820
8	9.756	9.757	9.762	9.768	9.777	9.786	9.794	9.801	9.806	9.807
12	9.743	9.745	9.749	9.756	9.765	9.774	9.782	9.789	9.794	9.795
16	9.731	9.732	9.737	9.744	9.752	9.761	9.770	9.777	9.781	9.783
20	9.719	9.720	9.725	9.732	9.740	9.749	9.757	9.764	9.769	9.770

註：如果上升高度不大,則每升1km，g 減少0.03%。

重力加速度g不同單位制之間的換算關係為：重力加速度g = 9.81m/s^2;= 981cm/s^2; = 32.18ft/s^2;

註：圖為測量的一種重力加速度試驗單

月球表面的重力加速度約為1.62 m/s^2;，約為地球重力的六分之一

△g緯=8.14sin2φ×D（φ為緯度值，D為緯向距離、在北半球向北為正），即在北緯45°附近向北一公里 g增大8.14g.u.=8.14×10^-6m/s^2

△g高=-3.086△h（g.u.），即高度差距不太大時，每升高1米g減小3.086g.u.=3.086×10^-6m/s^2

精確計算

嚴格說來，質點受到萬有引力是質點的重力和質點隨地球繞自轉軸作勻速圓周運動產生向心力的矢量和。那么，重力就是質點受到萬有引力和質點隨地球繞自轉軸作勻速圓周運動產生向心力的矢量差。

假設地球質量是M，質點質量是m，質點所在緯度是θ，海拔高度h，此處的地球半徑是R，地球自轉的角速度是ω，萬有引力常數是G，質點和地球自轉軸之間的距離是r，那么顯然有r=(R+h)cosθ。此時，萬有引力F引=GMm/(R+h)^2，向心力F向=mrω^2=mω^2(R+h)cosθ

由余弦定理得G^2=F引^2+F向^2-2F引F向cosθ

具體公式見圖片。

上式是理論上的公式，實際套用可用下式

g=9.78049（1 + 0.0052884 (Sinθ）^2 - 0.0000059 *(Sin2θ） ^ 2） - 0.00000286h

計算方法

因為F= ,F=G=mg

所以g=GM/r^2（gr^2=GM被稱為黃金代換）

G：引力常量=6.67259*10^-11N㎡/kg^2(m^3/k·gs^2）

M：中心天體質量/千克

r：天體中心與物體中心的距離/m

g的單位是m/s^2或N/kg

精確的重力加速度

在近代一些科學技術問題中，需考慮地球自轉的影響。更精確地說，物體的下落加速度g是由地心引力F（見萬有引力）和地球自轉引起的離心力Q（見相對運動）的合力W產生的（圖1）。Q的大小為

m為物體的質量；ω為地球自轉的角速度； 為地球半徑；H為物體離地面的高度； 為物體所在的地球緯度。這個合力即實際見到的重力W=mg。地球重力加速度是垂直於大地水準面的。在海平面上g隨緯度 變化的公式（1967年國際重力公式）為：

在高度為H的重力加速度g（1930年國際重力公式）同H和 有關，即

式中H為以米為單位的數值。

最早測定重力加速度的是伽利略。約在1590年，他利用斜面將g的測定改為測定微小加速度a=gsinθ，θ是斜面的傾角。測量重力加速度的另一方式是阿脫伍德機。1784年，G. 阿脫伍德將質量同為M的重塊用繩連線後，放在光滑的輕質滑車上，再在一個重塊上附加一重量小得多的重塊m（圖2）。這時，重力拖動大質量物塊，使其產生一微小加速度，測得a後，即可算出g。後人又用擺和各種優良的重力加速度計測定g。

地球上幾個不同緯度處的g值見下表；從中可以看出g值隨緯度的變化情況：

由於地球是微橢球形的，加之有自轉，在一般情況下，重力加速度的方向不通過地心，重力加速度的測定，對物理學、地球物理學、重力探礦、空間科學等都具有重要意義。

逃逸速度

一個質量為m的物體具有速度v，則它具有的動能為mv^2/2。假設無窮遠地方的引力勢能為零（應為物體距離地球無窮遠時，物體受到的引力勢能為零，所以這個假設是合理的），則距離地球距離為r的物體的勢能為-mar(a為該點物體的重力加速度，負號表示物體的勢能比無窮遠點的勢能小）。又因為地球對物體的引力可視為物體的重量，所以有

GmM/r^2=ma

即a=(GM)/r^2.

所以物體的勢能又可寫為-GmM/r，其中M為地球質量。設物體在地面的速度為V，地球半徑為R，則根據能量守恆定律可知，在地球表面物體動能與勢能之和等於在r處的動能與勢能之和，即

mV^2/2+(-GMm/R)=mv^2/2+(-GmM/r）。

當物體擺脫地球引力時，r可看作無窮大，引力勢能為零，則上式變為

mV^2/2-GmM/R=mv^2/2.

顯然，當v等於零時，所需的脫離速度V最小，即

V=2GM/R開根號，

又因為

GMm/R^2=mg,

所以

V=2gR開根號，

另外，由上式可見逃逸速度（第二宇宙速度）恰好等於第一宇宙速度的根號2倍。

其中g為地球表面的重力加速度，其值為9.8牛頓/千克。地球半徑R約為6370千米，從而最終得到地球的脫離速度為11.17千米/秒。

不同天體有不同的逃逸速度，脫離速度公式也同樣適用於其他天體。

天體計算

宇宙總是那么奧妙無窮，我們知道天體的質量非常大，人們又是如何測量出天體的質量的呢？

一、 用萬有引力定律和牛頓運動定律估算天體質量

在天體運動中，近似認為天體的運動是勻速圓周運動，在其運動過程中起決定因素的是萬有引力，即萬有引力提供天體做勻速圓周運動所需的向心力，有G(mM/r2）=m × （2π/T)2×r 其中周期可通過天文觀測方式獲得，從而可得天體質量為：M = [（2π/T)2×r3] / G

二 . 用萬有引力計算天體軌道.

在天文尺度下物體的運動服從經典理論，因此可以從已知的邊界條件（速度，位置，自旋）然後通過經典力學公式推算天體軌道，一個著名的例子是太陽系行星海王星的預測.（詳見中文百科詞條：海王星）

參考文獻

1、詞條作者：高為炳．《中國大百科全書》74卷（第一版）力學 詞條：重力加速度：中國大百科全書出版社，1987 ：596-597頁．