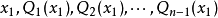線性變換群(group of linear transformations )一種重要的非交換群。
群是一種只有一個運算的、比較簡單的代數結構；是可用來建立許多其他代數系統的一種基本結構。
交換群是指其運算適合交換律的群，或稱阿貝爾群。挪威數學家阿貝爾在研究高次方程的根式求解時，除了五次方程以外，他討論了更廣一類的方程，現稱之為阿貝爾方程。
基本介紹
- 中文名：線性變換群
- 外文名：group of linear transformations
- 領域：代數
- 性質：非交換群
- 方式：線性變換
- 特點：不滿足交換律
- 相關概念：交換群
概念介紹,群,交換群,方式——線性變換,相關概念——變換群,
概念介紹
線性變換群(group of linear transformations )一種重要的非交換群。設V是域F上的n維向量空間，用GL(V)表示V的所有一一線性變換的集合。若在GL(V)中把映射的合成作為運算，則GL(V)對於該運算成為一個群，稱為線性變換群。
群
群是一種只有一個運算的、比較簡單的代數結構；是可用來建立許多其他代數系統的一種基本結構。
設G為一個非空集合，a、b、c為它的任意元素。如果對G所定義的一種代數運算“·”(稱為“乘法”，運算結果稱為“乘積”)滿足：
(1)封閉性，a·b∈G;
(2)結合律，即(a·b)c = a·(b·c);
(3)對G中任意元素a、b，在G中存在惟一的元素x，y，使得a·x= b，y·a=b，則稱G對於所定義的運算“·”構成一個群。例如，所有不等於零的實數，關於通常的乘法構成一個群;時針轉動(關於模12加法)，構成一個群。
滿足交換律的群，稱為交換群。
群是數學最重要的概念之一，已滲透到現代數學的所有分支及其他學科中。凡是涉及對稱，就存在群。例如，可以用研究圖形在變換群下保持不變的性質，來定義各種幾何學，即利用變換群對幾何學進行分類。可以說，不了解群，就不可能理解現代數學。
交換群
交換群是指其運算適合交換律的群，或稱阿貝爾群。挪威數學家阿貝爾在研究高次方程的根式求解時，除了五次方程以外，他討論了更廣一類的方程，現稱之為阿貝爾方程。其全部根都是其中一個根的有理函式，設x1是n次阿貝爾方程的一個根，其全部根則為
，其中Qi(i=1，…，n-1)是有理函式，並且對於任意的1≤i≤j≤ n，有Qi(Qj(x1))=Qj(Qi(x1))。後人發現，阿貝爾方程是具有交換律的伽羅瓦群的方程。為了紀念阿貝爾，後人稱交換群為阿貝爾群。
交換群是一般群論中的一個獨特分支。在拓撲學和代數學中常常構造一些交換群，作為討論問題的工具。例如，拓撲學中的基本群、同調群，代數學中的布饒爾群等等。交換群論與代數拓撲學、模論、同調代數、環論等有著密切的聯繫。
方式——線性變換
線性變換是線性代數的重要概念之一。設σ是數域P上的線性空間V的一個變換。若對於V中的任意向量α，β與P中的任意數k，有σ(α+β)=σ(α)+σ(β)，σ(kα)=kσ(α)，則稱σ是V的一個線性變換。設σ是線性空間V的一個變換，若對於V中任意向量α，有σ(α)=α，則σ是V的線性變換，稱為恆等變換，亦稱單位變換，記為I。若V的變換σ對於V中的任意向量α，有σ(α)=0，則σ是V的線性變換，稱為零變換，記為0。線性變換是歐氏幾何中的變換、解析幾何中的某些坐標變換、數學分析中的某些變數代換以及其他數學分支中某些類似的變換的抽象、概括與推廣。數域上線性空間的線性變換可以推廣為同一個域上的兩個不同線性空間的線性映射。線性變換不僅是線性代數的主要研究對象之一，也是數學中的一個重要的概念。近代數學中的許多分支的研究對象，如泛函分析中的線性運算元.同調代數中的模同態等都與線性變換有密切的聯繫。
相關概念——變換群
變換群是幾何學研究的重要對象。即由變換構成的群。設G是集合S的一一變換所構成的集合，若它滿足：
1.集合內任二變換之積仍屬於這集合；
2.集合內任一變換的逆變換仍屬於這集合，
則稱G為S的一個變換群。例如，平面上正交變換的全體構成的變換群稱為正交群；平面上仿射變換的全體構成的變換群稱為仿射群。平面上射影變換的全體構成的變換群稱為射影群。在“埃爾朗根綱領”中，變換群可用來對幾何學進行分類。
一組變換，對變換的乘積構成的群.設G為M上的有限或無限個變換的集合，若滿足下面兩個條件：①集合G中任意兩個變換的乘積仍屬於G;②集合G中每一個變換必有其逆變換，而且這個逆變換也屬於G，則稱G為M上的一個變換群。
例如，平移變換可以構成一個群：平面上任意兩個平移變換的積仍是平移變換;每個平移變換都有逆變換，這個逆變換就是按原變換相反方向的變換，所以仍是平移變換。
用變換群來研究對應的幾何學的觀點，是由德國數學家克萊茵首先提出來的.1872年，克萊茵在埃爾朗根大學的教授就職演講中，提出題為《關於近代幾何研究的比較》的論文，論述了變換群在幾何中的主導作用.他把到當時為止已發現的所有的幾何，統一在變換群的觀點之下，明確地給出了幾何的一種新定義，即把幾何定義為在某個變換群之下研究圖形不變性質與不變數的一門科學.這種觀點突出了變換群在研討幾何中的地位，為用近代數學方法研究幾何學開闢了道路，因此後來把它簡稱為《埃爾朗根綱領》。
按照變換群的觀點，幾何學可以這樣分類：研究射影變換群、仿射變換群、相似變換群、正交變換群下不變性質和不變數的幾何學分別是射影幾何學、仿射幾何學、拋物幾何學、歐氏幾何學。正交變換群也稱為運動群，歐氏幾何學的主要內容就是研究運動群下不變性質和不變數的幾何學。近代發展很快、套用越來越廣的一門學科——拓撲學，就是研究拓撲變換下不變性質和不變數的幾何學。
