線性李群(linear Lie group)一種重要的李群.由可逆線性變換構成的李群.設F為實數域或複數域。
線性李群(linear Lie group)一種重要的李群.由可逆線性變換構成的李群.設F為實數域或複數域,gl(n,F)為域F上所有n階方陣構成的集合,g1(二,F)一屍ZF.)-F.n為歐幾里得空間.gl(n,F)中所有n階非異方陣構成之子集合是g1 (n,F)中開子集,且在方陣乘法下構成一個nz維李群,記為GL(n,F),稱為一般線性群.GL(n,F)中任一李子群稱為矩陣李群.設GCGI_(n,F')為矩陣李群,屍為G的李代數,則可取聲Cgl(n,F).於是,若任取XE尹,則
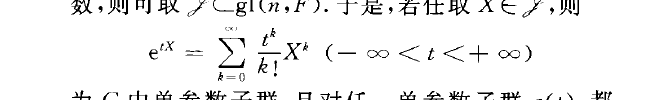
為G中單參數子群.且對任一單參數子群a(t),都存在XE聲,使得e`x=a(t),d tER.若F為實數域或複數域,則gl(V)中所有非異線性變換構成之集合G工一(V)線上性變換之乘法下構成一個李群.將GI_(V)之任一李子群稱為線性李群.在V中取定基後,V上線性變換惟一對應n階方陣.於是,矩陣李群為線性李群的矩陣表示.
