基本介紹
- 中文名:算術-幾何平均值不等式
- 簡稱:算幾不等式
介紹




證明







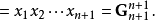
例子

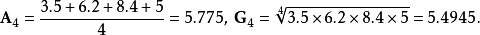

推廣














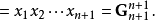

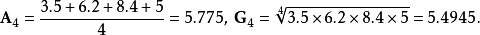




算術-幾何平均值不等式,簡稱算幾不等式,是一個常見而基本的不等式,表現了算術平均數和幾何平均數之間恆定的不等關係。...
算術-幾何平均不等式(inequality of arithmeticand geometric mean)著名經典不等式之一設ai,az}...}a,,均為正數,則它們的算術平均值不小於它們的幾何平均值,即...
均值不等式,又名平均值不等式、平均不等式,是數學中的一個重要公式。公式內容為Hn≤Gn≤An≤Qn,即調和平均數不超過幾何平均數,幾何平均數不超過算術平均數,算術...
算術-幾何平均是一種特殊平均,即算術平均與幾何平均的合成平均,設a0=a>b=b0>...3. 陳超平.平均值與г函式不等式:大象出版社,2009.09:第18頁圖集...
n個正數的算術平均值與幾何平均值的比較。...... n個正數的算術平均值與幾何平均值的比較。設 為n個正數,則其算術平均值不小於其幾何平均值,即...
利用琴生不等式法也可以很簡單地證明均值不等式,同時還有柯西歸納法等方法。平均數不等式參見 編輯 算術-幾何平均值不等式 冪平均不等式 ...
均值定理,又稱基本不等式。主要內容為在正實數範圍內,若干數的幾何平均數不超過他們的算術平均數,且當這些數全部相等時,算術平均數與幾何平均數相等。均值定理是...
基本不等式是主要套用於求某些函式的最值及證明的不等式。其表述為:兩個正實數的算術平均數大於或等於它們的幾何平均數。...
楊氏不等式又稱Young不等式 ,Young不等式是加權算術-幾何平均值不等式的特例,Young不等式是證明Holder不等式的一個快捷方法。...
算術-幾何平均是一種特殊平均,即算術平均與幾何平均的合成平均,設a0=a>b=b0>...2. 陳超平.平均值與г函式不等式:大象出版社,2009.09:第18頁圖集 合成平均圖冊...
- 調和平均(-1次冪), -幾何平均(0次冪), - 算術平均(1次冪),, - 二次平均(2次冪)重要不等式權方和不等式 編輯 1)a1 ^ (m+1) / b1^m + a2 ...
這個不等式即凸性不等式,也常稱為延森不等式。凸性不等式推廣 編輯 當 ,並且令 ,上式變為“幾何平均不大於算術平均”不等式:延森不等式的積分形式在套用上極...
第9章 不等式的證明方法[附] 算術平均值一幾何平均值不等式證法第10章 自然數方冪和的求法[附] 級數求和方法第11章 要識廬山真面目——解剖幾個習題...
條件不等式 矛盾不等式 克萊姆法則 算術平均數 幾何平均數一元多項式 乘法單調性 加法單調性 最小正周期 零次多項式待定係數法 輾轉相除法 二項式定法二項展開式...
對勾函式性質的研究離不開均值不等式。說到均值不等式,其實也是根據二次函式得...也是平均數的公式,但不同的是,前面的稱為算術平均數,而後面的則稱為幾何平均...
第6章 不等式 §6.1不等式的基本性質 知識點對接 大班數學活動:數字比大小 中班數學活動:比較高矮 §6.2算術平均數與幾何平均數 §6.3一元一次不等式組的解...
第一講不等式的概念和性質 第二講算術平均數與幾何平均數 第三講不等式的證明 第四講不等式的解法 第六章直線和圓的方程 第一講直線的傾斜角、斜率、...
