合成平均是一種特殊平均,設a>b>0,a0=a,b0=b,an,bn(n=1,2,…)分別是an-1與bn-1的算術平均與調和平均,則limn→∞an=limn→∞bn=√(ab),這說明幾何平均可以通過算術平均與調和平均構成的數列得到,這種思想的一般化就是合成平均。
基本介紹
- 中文名:合成平均
- 所屬學科:數學
- 簡介:幾何平均、調和平均等的合成
- 舉例:算術幾何平均
基本介紹













舉例說明


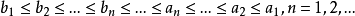




合成平均是一種特殊平均,設a>b>0,a0=a,b0=b,an,bn(n=1,2,…)分別是an-1與bn-1的算術平均與調和平均,則limn→∞an=limn→∞bn=√(ab),這說明幾何平均可以通過算術平均與調和平均構成的數列得到,這種思想的一般化就是合成平均。















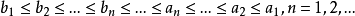



合成平均是一種特殊平均,設a>b>0,a0=a,b0=b,an,bn(n=1,2,…)分別是an-1與bn-1的算術平均與調和平均,則limn→∞an=limn→∞bn=√(ab),這說明幾何...
算術-幾何平均是一種特殊平均,即算術平均與幾何平均的合成平均,設a0=a>b=b0>0,an=1/2(an-1+bn-1),bn=√(an-1·bn-1),則an和bn有共同的極限,這個...
平均臉是一個整容專業辭彙,指經過計算機技術處理得到的某一群體的合成性容貌。長著平均臉的一群人在很大程度上有著相似的相貌,使出現撞臉的機會大大增加。...
合成指數亦稱“景氣綜合指數”。由一類特徵指標以各自的變化幅度為權數的加權綜合平均數。即多個指標的加權平均。能預測經濟周期波動的轉折點,並能在某種意義上反映...
“平均相貌”是由格拉斯哥大學的研究人員採用高爾頓的“合成肖像法”將世界各國數百名女性照片用電腦疊加在一起一個實驗研究。結果顯示被指脫離現實。...
平均風是一定觀測時段風向、風速的平均值。...... 簡單的做法是分別對風向和風速求算術平均值,嚴格意義上應是此時段內各時刻順時風的矢量合成的平均,以直角坐標三...
平均相貌是由格拉斯哥大學的研究人員對世界各國女性的平均長相做了一個研究,他們把每個國家數百名女性的照片用電腦疊加在一起,做成了一份41個國家的平均長相圖。...
合成風是根據風向量的分量相加求得的向量和。設有n個風向量,要求其合成風,先將各個風向量分解成分量,然後求其分量之和,再把各分量之和合併為向量和。這個向量...
雙官能度的小分子單體,通過縮聚反應生成線形聚合物,同時伴隨著小分子副產物生成的聚合過程稱之線形縮聚反應,簡稱為線性合成。...
合成類固醇又被稱為雄性合成類固醇激素,同化類固醇,促蛋白合成類固醇,包括皋酮及其衍生物。它與存在於機體性器官、肝、心、大腦、肌肉等部位的雄性激素受 體( AR ...
合成謬誤(Fallacy of Composition)是薩繆爾森提出來的。意即,它是一種謬誤,對局部說來是對的東西,僅僅由於它對局部而言是對的,便說它對總體而言也必然是對的。...
全基因合成:一般對於分子較小而又不易得到的基因採用該方式。可將X鏈基因分成若干寡核苷酸單鏈片段(尤其待合成基因在100 個核苷酸以上時),每個片段長度控制在40~60...
概述速度評比、平準化法和客觀評比,都不同程度地帶有觀測人員的主觀判斷,1946年美國工業工程大師莫羅(R.L.Morrow)為了克服此困難,創立了“合成評比法”。 合成...
合成佯謬,經濟學術語,是指把局部合理的經濟學判斷,簡單地匯加起來,可能導致全局錯誤的結論。...
碳氮鍵的鍵長數值也相近,鍵角約為120°,這說明吡啶環上鍵的平均化程度較高,...Boger 吡啶合成化學性質 吡啶及其衍生物比苯穩定,其反應性與硝基苯類似。典型的...
相干合成的技術方案按是否通過外界手段來干預探測並校正相位誤差可分為主動式的閉環有源相位控制和被動式的自組織鎖相運行雷射器陣列兩大類。...
電漿合成又稱放電合成,是20世紀70年代才迅速發展起來的一種技術手段。它是利用電漿特殊性質進行化學合成的一種新技術。電漿是由電子、原子、分子、自由...
合併樣本標準差是指為了提高不確定評定的可靠性,需要取若干樣本,每個樣本均用貝塞爾法計算出樣本的實驗標準差sj,然後將各個sj進行合併(或平均),以sp表示。...
