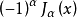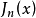基本概念
是數學上的一類特殊函式的總稱。一般貝塞爾函式是下列
常微分方程(一般稱為
貝塞爾方程)的標準解函式
:
這類方程的解無法用初等函式系統地表示。
貝塞爾函式的具體形式隨上述方程中任意
實數 變化而變化(相應地,
被稱為其對應貝塞爾函式的階數)。實際套用中最常見的情形為
是整數
,對應解稱為
n階貝塞爾函式。
儘管在上述微分方程中,
本身的正負號不改變方程的形式,但實際套用中仍習慣針對
和
定義兩種不同的貝塞爾函式(這樣做能帶來好處,比如消除了函式在
點的不光滑性)。
基本內容
貝塞爾函式(Bessel functions)是數學上的一類特殊函式的總稱。一般貝塞爾函式是下列
常微分方程(一般稱為'''貝塞爾方程''')的標準解函式。
這類方程的解無法用
初等函式系統地表示。但是可以運用自動控制理論中的相平面法對其進行定性分析。
這裡,
被稱為其對應貝塞爾函式的
階數。實際套用中最常見的情形為
是整數,對應解稱為
階貝塞爾函式。
儘管在上述微分方程中,本身的正負號不改變方程的形式,但實際套用中仍習慣針對 和
定義兩種不同的貝塞爾函式(這樣做能帶來好處,比如消除了函式在
點的不光滑性)。
定義
貝塞爾方程是一個二階常微分方程,必然存在兩個線性無關的解。針對各種具體情況,人們提出了這些解的不同形式。下面分別介紹不同類型的貝塞爾函式。
歷史
現實背景和套用範圍
貝塞爾方程是在柱坐標或球坐標下使用分離變數法求解
拉普拉斯方程和
亥姆霍茲方程時得到的,因此貝塞爾函式在波動問題以及各種涉及有勢場的問題中占有非常重要的地位,最典型的問題有:
* 在圓柱形波導中的
電磁波傳播問題;
* 圓柱體中的熱傳導定律|熱傳導問題;
* 圓形(或環形)薄膜的振動
模態分析問題;
貝塞爾函式的實例:一個緊繃鼓面在中心受到敲擊後的二階振動振型,其振幅沿半徑方向上的分布就是一個貝塞爾函式(考慮正負號)。實際生活中受敲擊的鼓面的振動是各階類似振動形態的疊加。
第一類貝塞爾函式
第一類
階貝塞爾函式
是貝塞爾方程當
為整數或
非負時的解,須滿足在
時有限。這樣選取和處理''J''<sub>α</sub>的原因見本主題下面的貝塞爾函式#性質|性質介紹;另一種定義方法是通過它在
點的
泰勒級數展開(或者更一般地通過
冪級數展開,這適用於α為非整數):
上式中
為Γ函式(它可視為
階乘|階乘函式向非整型
因變數和自變數|自變數的推廣)。第一類貝塞爾函式的形狀大致與按
速率衰減的正弦或三角函式|餘弦函式類似(參見本頁下面對它們漸進形式的介紹),但它們的零點並不是
周期性的,另外隨著''x''的增加,零點的間隔會越來越接近周期性。圖2所示為0階、1階和2階第一類貝塞爾函式
的曲線(
)。
如果
;不為整數,則
和
線性無關,可以構成微分方程的一個'''解系'''。反之若
是整數,那么上面兩個函式之間滿足如下關係:
=
於是兩函式之間已不滿足線性無關條件。為尋找在此情況下微分方程與
線性無關的另一解,需要定義'''第二類貝塞爾函式'''。
第二類貝塞爾函式(諾依曼函式)
'''第二類貝塞爾函式'''也許比第一類更為常用。這種函式通常用表示,它們是貝塞爾方程的另一類解,又被稱為'''諾依曼函式''',存在如下關係:
,
漢開爾函式
貝塞爾方程的另外一對重要的線性無關解稱為'''赫爾曼·漢開爾,漢開爾函式''',分別定義為:
利用前面推出的關係可將漢開爾函式表示成:
黎卡提-貝塞爾函式
黎卡提-貝塞爾函式(Riccati-Bessel functions)和球貝塞爾函式比較類似:
分類
利用柱坐標求解涉及在圓、球與圓柱內的勢場的物理問題時出現的一類特殊函式。又稱標函式。用柱坐標解
拉普拉斯方程時,用到貝塞爾函式,它們和其他函式組合成柱調和函式。除初等函式外,在物理和工程中貝塞爾函式是最常用的函式,它們以19世紀德國天文學家F.W.貝塞爾的姓氏命名,他在1824年第一次描述過它們。貝塞爾函式最早出現在涉及如懸鏈振盪,長圓柱體冷卻以及緊張膜振動的問題中。貝塞爾函式的一族,也稱第一類貝塞爾函式,記作
,用
的偶次冪的無窮和來定義,數
稱為貝塞爾函式的階,它依賴於函式所要解決的問題。
的圖形像衰減的
餘弦曲線,
像衰減的
正弦曲線(見圖)。
第二類貝塞爾函式(又稱諾伊曼函式),記作
。當n為非整數時,
可以由第一類貝塞爾函式的簡單組合來定義;當
為
整數時,
不能由第一類貝塞爾函式的簡單組合得到,此時需要通過一個求極限過程來計算
函式值。
第三類貝塞爾函式(亦稱漢克爾函式)定義為
,其中
為虛數,用n階(正或負)貝塞爾函式可解稱為貝塞爾方程的微分方程。
套用範圍
貝塞爾方程是在
柱坐標或
球坐標下使用
分離變數法求解拉普拉斯方程和
亥姆霍茲方程時得到的(在圓柱域問題中得到的是整階形式 α = n;在球形域問題中得到的是半奇數階形式 α = n+½),因此貝塞爾函式在波動問題以及各種涉及有勢場的問題中占有非常重要的地位,最典型的問題有:
在其他一些領域,貝塞爾函式也相當有用。譬如在
信號處理中的
調頻合成(
FMsynthesis)或
凱澤窗(Kaiser window)以及波動聲學中都要用到貝塞爾函式。