一種特殊的有理函式逼近,也是非線性近似的一種方法,是以法國數學家H.帕德的名字命名。
基本介紹
- 中文名:帕德逼近
- 外文名:Pade'Approximant
- 發明人:亨利·帕德
- 性質:有理多項式近似法
簡介,定義,例子,正弦函式,指數函式,雅可比橢圓函式,第一類 5 階貝塞爾函式,誤差函式,菲涅耳積分,
簡介
例如, 1/(1-x) 的泰勒級數
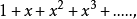
定義
給定兩個正整數m、n, 函式 階帕德近似為
階帕德近似為


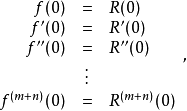
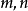
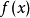

函式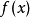 的帕德近似記為
的帕德近似記為
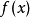
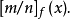
例子
正弦函式
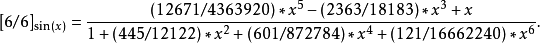
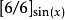
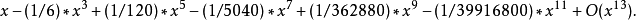
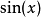

指數函式

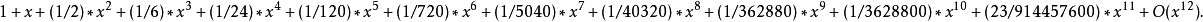

- 又如
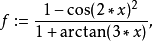
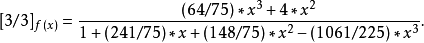
雅可比橢圓函式

第一類 5 階貝塞爾函式

誤差函式
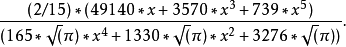
菲涅耳積分


