基本介紹
主要思想
常微分方程
第一種方法
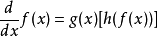
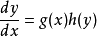
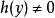

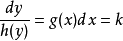
第二種方法
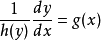
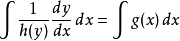
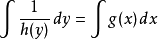
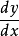
偏微分方程
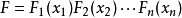
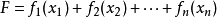

例子
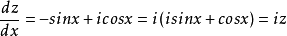
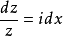
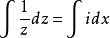
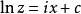
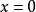
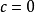
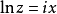
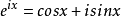

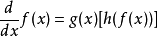
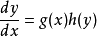
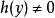

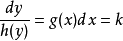
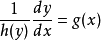
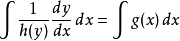
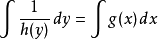
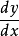
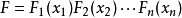
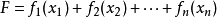

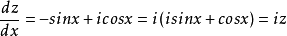
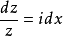
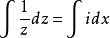
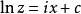
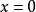
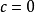
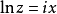
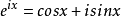
分離變數法是將一個偏微分方程分解為兩個或多個只含一個變數的常微分方程。將方程中含有各個變數的項分離開來,從而將原方程拆分成多個更簡單的只含一個自變數的...
用來求得解析解的方法稱為解析法,解析法是常見的微積分技巧,如分離變數法等。解析解為一封閉形式的函式,因此對任一獨立變數,皆可將其代入解析函式求得正確的相依...
《高等傳熱學:導熱與對流的數理解析》共九章,主要內容包括:導熱問題的數學描述,用分離變數法求解導熱問題,用拉普拉斯變換求解非穩態導熱問題,用傅立葉變換法求解導熱...
球函式(spherical function)通常指連帶勒讓德方程的解,亦即連帶勒讓德函式。有時也把面調和函式稱為球函式。在球坐標系中用分離變數法解拉普拉斯方程或亥姆霍茲方程...
其中行波法主要適用於求解無界區域的齊次波動方程的定解問題;分離變數法適用於解波動法方程、輸運方程和穩定場方程等;積分變換法適用於無界區域或半無界區域的定解...
用來求得解析解的方法稱為解析法(Analytical techniques),解析法即是常見的微積分技巧,例如分離變數法等。解析解是一個封閉形式(Closed-form) 的函式,因此對任一...
2008 求解數理方程解析解的一種新方法:混合分離變數法 蔡睿賢,劉啟斌 中國科學(G輯)(第9期) 2008 一維非定常完全氣體熱聲流的代數顯式解析解 蔡睿賢,劉啟斌 工...
7.4 變分法 2347.4.1 泛函和泛函的極值 2347.4.2 里茲方法 2377.5 本章小結240第8章 數學物理方程的可視化計算 2418.1 分離變數法的可視化計算 241...
3-2 有限厚度物體的非穩態導熱:分離變數法3-3 半無限大物體的非穩態導熱:相似性解和積分近似解3-4 格林函式法在非穩態導熱中的套用...
書中全面系統論述作者及其課題組近幾年建立的新研究方法,如多線性分離變數法、泛函分離變數法和導數相關泛函分離變數法、形變映射法、方程推導的非平均法等。本書...
數值解,是指給出一系列對應的自變數,採用數值方法求出的解。採用的方法有限元法、數值逼近、插值法。他人只能利用數值計算的結果,而不能隨意給出自變數並求出計算...
靜電場的唯一性定理可以用來直接或間接求解靜電場,如常用的試探法、鏡像法求解靜電場,而其他求解靜電場的常規方法如分離變數法和格林函式法,在求解靜電場時以解析法...
本書尤為注重幾何直觀的引導作用,儘量以平面和函式空間為背景闡述全書內容,對數學物理方程的常用解法,諸如分離變數法和積分變換法等的原理都做出了幾何解釋。並且,從...
於是,可用分離變數法求方程(2)的精確解,圓球、雙圓球、橢球的無界繞流問題以及單個圓球垂直地向一無界平面運動的問題等都可用分離變數法求精確解。...
21.李卓球,張雄,張江濤 焦耳內熱源溫度場求解的分離變數法 武漢理工大學學報. 26(11).71-73,2004,EI收錄22.徐東亮,李卓球,宋顯輝,呂泳 機敏混凝土ERT實驗系統...
例題涉及複變函數及其積分和級數展開、複變函數的多值性、留數在積分中的套用、保角映射、數學物理問題的建立、本徵值問題、分離變數法、線性常微分方程的級數解法...
本書主要內容包括偏微分方程的基本概念、三類典型方程的導出與定解問題、特徵線積分法、傅立葉級數理論、分離變數法、格林函式法、積分變換法、極值原理與套用、能量...
13.1.3二維矩形區域內拉普拉斯方程的分離變數13.1.4二維圓形區域內拉普拉斯方程的分離變數13.2非齊次泛定方程的分離變數13.2.1本徵函式展開法...
求微分方程通解的方法有很多種,如:特徵線法,分離變數法及特殊函式法等等。而對於非齊次方程而言,任一個非齊次方程的特解加上一個齊次方程的通解,就可以得到非...
1941年J.A.斯特拉頓和朱蘭成利用長橢球坐標,對中間旋轉對稱饋電的、偏心率接近於1的長橢球形天線進行了理論分析,套用分離變數法並根據邊界條件直接求解麥克斯韋方程而...
了無窮多Lax對和非局域對稱理論;給出了多種意義下的高維可積模型;在實驗上觀察到了巨觀格點體系的多種孤子激發模式;建立了多線性分離變數法和導數泛函分離變數法...
對於分層界面為介質-導體混合結構的情況(如微帶線中導帶所在的基片表面),譜域法繞過了該界麵條件不適合直接用分離變數法求解的困難,從該常微分方程邊值問題的譜...
在p=0、p=1的附近變化幅度較大,用分離變數法解(1)式得到:反過來看(2)式,實質上是將事件A發生的機率p與不發生的機率1一p相比(稱為機率比)然後取對數。我們...
