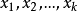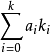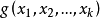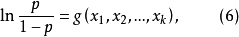羅吉斯蒂克變換

羅吉斯蒂克變換(logistic 變換)也稱羅吉脫變換，對因變數本身的指示變數、而回歸函式又為羅吉斯蒂克函式時適用的一種形如Z=ln(P/(1-P))的數學變換，通過一種這種數字變換使原函式線性化，成為Z的線性函式，從而可以用最小二乘法進行回歸估計。

基本介紹

• 中文名：羅吉斯蒂克變換
• 外文名：logistic transformation
• 別名：羅吉脫變換，logistic變換等
• 所屬學科：數學（數理科學）
• 相關概念：羅吉斯蒂克模型、logistic函式等

定義

羅吉斯蒂克變換（logistic 變換）也稱羅吉脫變換，羅吉斯蒂克函式

是一種非線性函式，通過一種形加

的數字變換使原函式線性化，成為Z的線性函式，從而可以用最小二乘法進行回歸估計，這種變換稱為羅吉斯蒂克變換。

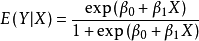
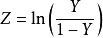
logistic變換與logistic回歸

在現實問題中，人們常常要研究某一事件A發生的機率p以及p值的大小與某些因素的關係，但在許多情況下，變數x的變化，使機率在p=0或p=1的附近的變化較緩慢，很少有確定的p=0或p=1出現，於是自然的一個想法是希望尋找一個關於p的函式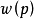，要求它在p=0和p=1附近變化幅度較大且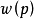的表現形式較簡單，根據這一構想研究者提出用導數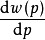在反映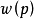在p附近的變化，取

顯然時，；當時，。這說明在p=0、p=1的附近變化幅度較大，用分離變數法解(1)式得到：

反過來看(2)式，實質上是將事件A發生的機率p與不發生的機率1一p相比(稱為機率比)然後取對數。我們就稱(2)式為Logistic變換。由(2)式解出：

(3)式與Logistic函式(邏輯斯蒂函式)類似，該函式在研究生物的繁殖及人口估計和預測中有著廣泛的套用。我們分析(3)式可以看到該函式有如下特徵。

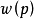
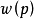
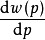
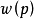
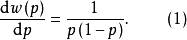
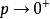
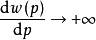
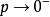
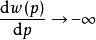
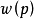
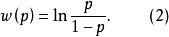
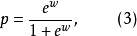
(1)無論w變化如何，其因變數p∈(0，1)當p=1和p=0時為(3)式兩條水平漸近線，說明(3)的曲線圖形夾在p=0和p=1兩條漸近線之間。

(2)(3)式所表示的圖形嚴格單調增函式，表明不同的y對事件發生的每個機率各不相同。同時，函式增長的特點先慢，後快，然後再趨向緩慢。大量事實表明，logistic函式的這些特徵與社會生活中的許多現象較相符，它說明用logistic回歸來描述事物發生的機率是可行且合理的。

如果w是某些自變數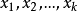的線性函式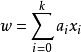，這時(3)式就變為下式：

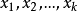
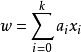
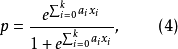
或者為：

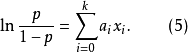
(5)式的右端保留了關於自變數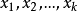的線性性質，而左端不再是線性回歸中的y，而是隨機變數y，發生機率P(y=1)=p與不發生機率1-p之比的對數。我們把(5)稱為廣義線性logistic回歸。如果(5)的右邊不是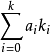，而是已知函式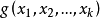，其中含有若干待定的參數，使下式(6)成立。

稱(6)為非線性logistic回歸。