基本介紹
- 中文名:笛卡爾坐標系
- 外文名:Cartesian coordinates
- 領域:數學
- 釋義:直角坐標系和斜坐標系的統稱
- 屬性:一種仿射坐標系
- 推廣:空間笛卡爾坐標系
坐標系簡介
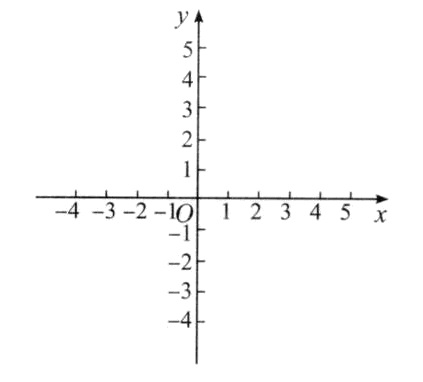
二維坐標系
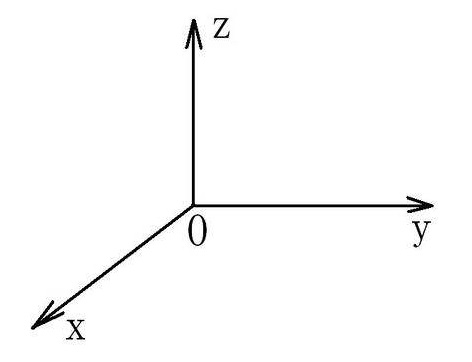
三維坐標系
產生過程
電影定義


笛卡爾坐標一般指本詞條




笛卡爾坐標系(Cartesian coordinates)(法語:les coordonnées cartésiennes)就是直角坐標系和斜角坐標系的統稱。 相交於原點的兩條數軸,構成了平面放射坐標系。如兩條數軸上的度量單位相等,則稱此放射坐標係為笛卡爾坐標系。兩條數軸互相垂...
笛卡爾坐標系(Cartesian Coordinates)就是直角坐標系和斜角坐標系的統稱。相交於原點的兩條數軸,構成了平面仿射坐標系。如兩條數軸上的度量單位相等,則稱此仿射坐標係為笛卡爾坐標系。兩條數軸互相垂直的笛卡爾坐標系,稱為笛卡爾直角坐標...
在數學裡,笛卡爾坐標系(英語:Cartesian coordinate system),也稱直角坐標系,是一種正交坐標系。參閱圖1,二維的直角坐標系是由兩條相互垂直、相交於原點的數線構成的。在平面內,任何一點的坐標是根據數軸上對應的點的坐標設定的。...
在笛卡爾的時代,拉丁文是學者的語言。他也如當時的習慣,在他的著作上籤上他的拉丁化的名字——Renatus Cartesius(瑞那圖斯·卡提修斯)。正因為如此,由他首創的笛卡爾坐標系也稱卡提修坐標系。笛卡爾對結合數學與物理學的興趣,是在...
1.三維笛卡爾坐標 三維笛卡爾坐標(X,Y,Z)與二維笛卡爾坐標(X,Y)相似,即在X和Y值基礎上增加Z值。同樣還可以使用基於當前坐標系原點的絕對坐標值或基於上個輸入點的相對坐標值。2.圓柱坐標 圓柱坐標與二維極坐標類似,但增加了...
笛卡爾平面直角坐標系中平行於縱坐標軸的方向與某一方向的夾角。坐標方位角是平面直角坐標系中某一直線與坐標主軸(X軸正北向)之間的夾角,從主軸(X軸方向北,Y軸方向東)起算,順時針方向旋轉(範圍0~360度。)說明 以順時針為正...
橫坐標 橫坐標,平面笛卡爾坐標系中一個點的橫的坐標,由平行於x軸的線段來度量。詞性 abscissa 【計】 X-axis 【化】 abscissa 【經】 abscissa 解釋 橫坐標通常與縱坐標相對。在數學的函式中也有所套用。
三維坐標,是指通過相互獨立的三個變數構成的具有一定意義的點。它表示空間的點,在不同的三維坐標系下,具有不同的表達形式。簡介 三維笛卡爾坐標(X,Y,Z)是在三維笛卡爾坐標系下的點的表達式,其中,x,y,z分別是擁有共同的零點...
則 。推導過程 見《笛卡爾定理與一類多圓相切問題》(作者:王永喜、李奮平)。定理推廣 笛卡爾定理在三維坐標系中也有類似的結論:若五個球的半徑是r(1,2,...,5),滿足任意一個球與其他四個球外切,則 。
坐標系變換 1.時鐘坐標系(x',y',θ‘)與笛卡爾坐標系(x,y,z)的轉換關係:x=x'y=y'cosθ‘z=y'sinθ‘2.反之,笛卡爾坐標系(x,y,z)與時鐘坐標系(x',y',θ‘)的轉換關係:x‘=x y‘=ysecθ'θ‘=arc...
坐標轉化 編輯 語音 (1)極坐標系坐標轉換為平面直角坐標系(笛卡爾坐標系)下坐標:極坐標系中的兩個坐標 ρ和 θ可以由下面的公式轉換為直角坐標系下的坐標值: x=ρcosθ y=ρsinθ (2)平面直角坐標系坐標轉換為極坐標系下坐標:...
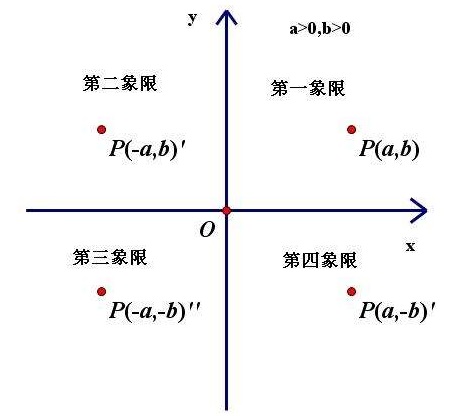
縱坐標(vertical ordinate),也稱y坐標,縱坐標與橫坐標構成笛卡爾坐標系(直角坐標系)以表示函式的圖像。用於計算某點到坐標軸的距離。定義 在點P(a,b)中a為橫坐標,b為縱坐標。性質 (a,b)到X軸的距離為|b|,到Y軸的距離...
笛卡兒在方法論中還第一次提出“我思故我在”的名言,第一次引入笛卡兒坐標系。對牛頓和萊布尼茨發明微積分理論有很大的作用。方法論出版 《方法論》(Discours de la méthode)是笛卡兒在1637年出版的著名哲學論著,對西方人的思維方式...
3.工件坐標系( Workpiece Coordinate System )固定於工件上的笛卡爾坐標系,是編程人員在編製程序時用來確定刀具和程式起點的,該坐標系的原點可使用人員根據具體情況確定,但坐標軸的方向應與工具機坐標系一致並且與之有確定的尺寸關係。機...
笛卡爾坐標系直角坐標系和斜角坐標系的統稱。直角坐標系和斜角坐標系的統稱。相交於原點的兩條數軸,構成了平面放射坐標系。如兩條數軸上的度量單位相等,則稱此放射坐標係為笛卡爾坐標系。兩條數軸互相垂直的笛卡爾坐標系,稱為笛卡爾直角...
象限,又稱象限角(英文:Quadrant意思是一圓之四分一等份),是直角坐標系(笛卡爾坐標系)中,主要套用於三角學和複數的阿根圖(複平面)中的坐標系。平面直角坐標系裡的橫軸和縱軸所劃分的四個區域,分為四個象限。象限以原點為中心...
pol2cart在MATLAB中, 該函式用於把極坐標(柱坐標)轉換為笛卡爾坐標(指平面直角坐標或空間直角坐標)。 語法格式: [X,Y] = pol2cart(THETA,RHO) 把極坐標(THETA,RHO)轉換為對應的二維笛卡爾坐標(X,Y)。 [X,Y,Z] = pol2cart(THETA...
cart2sph是一個函式。函式簡介 函式功能:在MATLAB中,該函式把笛卡爾坐標 轉換為對應的球坐標 。語法格式:把3維笛卡爾坐標 轉換為對應的球坐標 。其中 是向量 在 平面內投影與 軸正向沿逆時針方向的夾角,是向量 與 平面的夾角...
cart2pol是Matlab中的一個函式,作用為:將笛卡爾坐標轉換為極坐標。函式簡介 函式功能:在MATLAB中, 該函式用於把笛卡爾坐標轉換為極坐標(柱坐標)。語法格式:[THETA,RHO,Z] = cart2pol(X,Y,Z)把三維笛卡爾坐標(X,Y,Z)轉換為...
象限,又稱象限角(英文:Quadrant意思是一圓之四分一等份),是直角坐標系(笛卡爾坐標系)中,主要套用於三角學和複數的阿根圖(複平面)中的坐標系。平面直角坐標系裡的橫軸和縱軸所劃分的四個區域,分為四個象限。象限以原點為中心...
通用的從笛卡爾坐標繫到極坐標系的變換方法:根據最新的研究表明,阿基米德螺旋公式可以用指定的半徑r,圓周速度v,直線運動速度w來表示,公式為根據這一公式,當圓周速度與直線速度同時增大一倍時,阿基米德螺旋的形狀是不會發生變化的,因此,...
該曲線被定義在極坐標方程下,在笛卡爾坐標系,該曲線滿足的隱式方程 除了對於a=0以外,隱式方程形式存在一個孤立點(0,0)不存在於極坐標方程形式中。特徵 它們是有理曲線、循環代數曲線、三次曲線。這些表達式有一個漸近線x=1(a≠0...
狹義相對論中關於不同慣性系之間物理事件時空坐標變換的基本關係式。設兩個慣性係為S系和S′系,它們相應的笛卡爾坐標軸彼此平行,S′系相對於S系沿x方向運動,速度為v,且當t=t′=0時,S′系與S系的坐標原點重合,則事件在這兩...
REC 是計算機術語,全稱是Regional Echomail Coordinator,區內會議信件協調人。釋義 ●數學運算符號(求極坐標到直角坐標系的點轉化)與Pol相對。在計算器中一般是shift+Pol ●平面坐標轉化:極坐標系的點轉化到笛卡爾直角坐標系(即平面...
