基本介紹
- 中文名:積分非線性
- 外文名:Integral nonlinearity
- 簡寫:INL
- 簡介:模數轉換器的靜態性能參數
- 單位:LSB
- 相關概念:模數轉換器ADC、微分非線性等
基本介紹
相關概念
失調
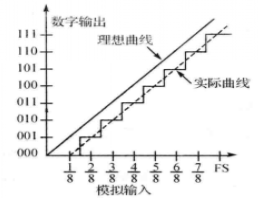
增益誤差
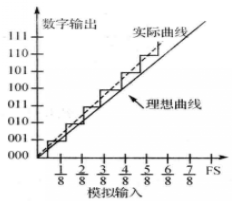
微分非線性
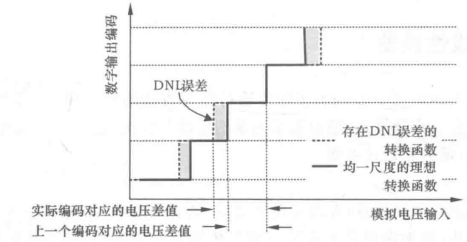
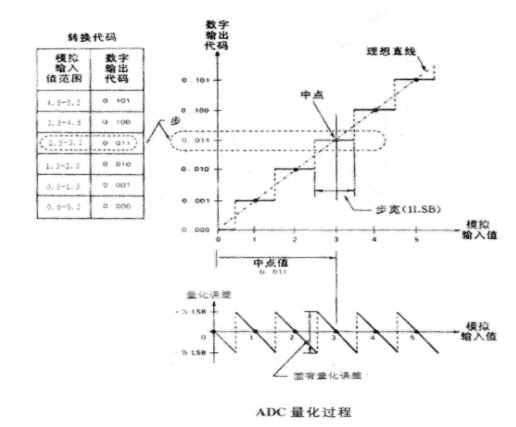




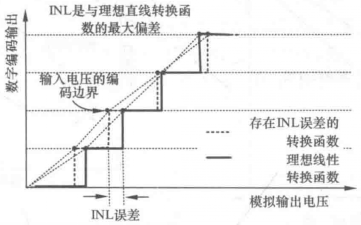
積分非線性(Integral Nonlinearity,INL)是模數轉換器的靜態性能參數之一,是指實際轉換曲線同理想轉換曲線在縱軸方向的差值,單位是LSB,即最低有效位。它表示實際轉換曲線偏離理想轉換曲線的程度。基本介...
非線性積分方程(nonlinear integral equation)是指不具有線性性質的一類積分方程。如果未知函式在積分號下是以非線性形式出現的,這種方程就稱為非線性積分方程。非線性積分方程也可以被分成多種類型,例如,弗雷德霍姆型、沃爾泰拉型、...
常見的非線性積分運算元有:烏雷松運算元 其中 k(x,y,t) 是 上的已知函式,它關於 t 是非線性的。沃爾泰拉運算元 其中k(x,y,t) 是 上的已知函式,它關於 t 是非線性的,a 哈默斯坦運算元 其中k(x,y) 是 上 p 冪可積...
《線性與非線性積分方程:方法及套用》是2011年6月1日高等教育出版社出版的圖書,作者是(美國)佤斯瓦茨(Abdul-Majid Wazwaz)。內容簡介 這是一本同時介紹線性和非線性積分方程的教材,分成兩部分,各部分自成體系。第一部分主要對第...
非線性沃爾泰拉積分方程是一個數學術語。非線性沃爾泰拉積分方程(nonlinear Volterraintegral equation)積分上限變動的一類特殊的非線性方程.這指的是如下方程 這時,對任意幾,方程(1)在z,`La,b內都存在著惟一解.
《基於非線性積分的可積函式空間及泛函表示》是依託湖州師範學院,由歐陽耀擔任項目負責人的面上項目。項目摘要 本項目研究三類重要非線性積分— Choquet積分、泛積分和凹積分的可積函式空間性質和基於這些積分的非線性泛函表示。主要內容為...
《多約束下非線性積分器系統魯棒自適應控制及套用》是依託北京大學,由王金枝擔任負責人的面上項目。項目摘要 本項目圍繞具有實際工程背景的不確定積分器非線性系統在不同約束限制下的幾個重要問題展開理論研究和基礎套用研究,具體包括三個...
《非線性微分方程積分邊值問題的研究》是2017年科學出版社出版圖書,作者是宋文晶、郭斌。內容簡介 本書主要介紹起源於血管疾病(動脈粥樣硬化、動脈瘤)、地下水流、種群動態、等離子物理、計算流體動力學(Computational Fluid Dynamics)等常...
B積分是在非線性光學中對於光非線性相位移的量測,是計算雷射光束中最不穩定空間頻率的指數成長程度,在數值上等效於延著雷射系統光軸的非線性相位移。若用多通道的雷射系統來計算非線性相互作用的累計量,其積分為:其中 是延著光軸的...
積分號下含有未知函式的方程。其中未知函式以線性形式出現的,稱為線性積分方程;否則稱為非線性積分方程。積分方程起源於物理問題。牛頓第二運動定律的出現,促進了微分方程理論的迅速發展,然而對積分方程理論發展的影響卻非如此。1823年,...
積分學也被推廣到一般運算元。黎曼積分的定義與普通函式的積分定義一樣,而勒貝格積分的推廣則分強、弱兩種,前者稱為博赫納積分,後者稱為佩蒂斯積分(見向量值積分)。常見的非線性積分運算元 烏雷松運算元 .其中K(x,y,t)是 0≤x,y≤1...
高斯積分是在機率論和連續傅立葉變換等的統一化等計算中有廣泛的套用。在誤差函式的定義中它也出現。雖然誤差函式沒有初等函式,但是高斯積分可以通過微積分學的手段解析求解。高斯積分(Gaussian integral),有時也被稱為機率積分,是...
本書是積分方程的入門教材或教學參考書·書中內容廣泛,除了包括線性積分方程的基本理論與解法外,還敘述了第一類Fredholm方程、積分方程的數值解法,此外對奇異積分方程、積分方程組及非線性積分方程等作了簡要的介紹·所涉及的內容,既有...
4.積分非線性:≤0.2%。5.折合到輸入端的噪聲:≤10μV。6.過載:過載200倍,在2.5倍非過載脈衝寬度處恢復至基線的 2%。7.輸入極性:正或負。 輸出極性:正 輸出阻抗50Ω。8.成形時間常數:0,0.5,1,2,3,4,5,...
《非線性方程組和多重積分泛函的正則性理論及其套用》是依託浙江大學,由洪敏純擔任項目負責人的青年科學基金項目。項目摘要 以高分子微孔濾膜為載體,偶聯亞氨基二乙酸,製備出銅離子金屬螯合吸附劑。研究了膜表面修飾、羥基活化、螯合劑...
積分曲線(integral curve)是1993年公布的數學名詞。定義 設M為光滑流形,𝖃M為M上向量場,X∈𝖃M,I為閉區間,曲線c:I→M為曲線,且滿足 =X∘c,則c為X的積分曲線。性質 若c,:I→M為X的積分曲線,滿足存在t₀∈I,...
積分下限 積分下限(lower limit of integral)是1993年公布的數學名詞。公布時間 1993年,經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
傳統的PID控制是誤差的比例、積分、微分三項的線性組合,它具有原理簡單、參數易於調整、魯棒性較強等特點,在工業過程控制中得到了廣泛的套用。但是對於一些複雜的系統,特別是非線性對象,PID控制器並不能得到滿意的效果。如果對傳統的PID...
本項目研究一般非線性動力系統的可積性與不可積性。對n維歐氏空間中的動力系統,我們將給出系統存在代數首次積分的一些必要條件以及部分代數可積的一些判定準則,同時利用所得結果研究擬齊系統的可積性與不可積性。由於數學物理中的很多...
非線性動態逆控制(Nonlinear dynamic inversion control )是通過動態系統的‘逆’的概念來研究一般非線性控制系統反饋線性化設計的一種方法。套用研究表明,動態逆是非線性控制中的一種較為有效的方法,對非線性剛體太空飛行器系統具有很好的跟...
通信術語中的非線性,即模擬調製系統中的非線性調製。非線性調製又稱為角度調製,其已調信號的頻譜和調製信號的頻譜結構有很大的不同,除了頻譜搬移外,還增加了許多新的頻率成分。非線性調製包括調頻(FM)和調相(PM)兩大類。概念...
全積分(complete integral) n個自變數的一階非線性偏微分方程的含有n個獨立常數的解.例如,兩個自變數的一階非線性方程 的包含兩個獨立常數的解 稱為方程(1)的全積分.在兩參數曲面族(2)中選取單參數曲面族,例如,b全積分(complete...
F(x)是該剖面周圍氣流的環流,c是常數,v是無窮氣流的速度,ω是依賴於剖面曲率和機翼扭曲的函式。普朗特積分微分方程只是在非嚴格意義的假設下才能以封閉形式求解。在一般情況下,它可以轉化為弗雷德霍姆積分方程。
可以指任意映射,例如有條件限制(給定初始值或邊界值)的微分或積分運算。如果 內含有對 的微分運算,此方程即是一個微分方程。分類 這些方程可分為兩類,一種是多項式方程,一種是非多項式方程。非線性代數方程 主條目:代數方程 ...
若設定積分項的初始狀態如下 式中,xe0為系統初始時刻的偏差。則在t=0時刻,由上面兩個式子得到 上式表明,通過設計積分項的初始值,就能使系統狀態在初始時刻處於滑模面上,不存在到達階段,保證了系統的魯棒性。套用 非線性積分滑模...
Integral在數學上的中文譯名為積分,即累積的分數。在天文學釋義是新一代γ射線望遠鏡的名字。數學釋義 積分,即累積的分數。網上,有很多的積分活動,如電子信箱積分,qq秀積分等:生活中,有會員卡積分等等優惠活動。在微積分中 積分是...
微積分是線性空間中思考問題的數學,它在處理非線性問題時聯繫問題變得較複雜。現實中最多的非線性問題是與對數相關的問題。例如:如果星光傳播中光子的能量有一非常小的損耗率,設光子單位時間損耗率為 H,在任一時刻t ,光子的能量為...
