非線性沃爾泰拉積分方程是一個數學術語。
基本介紹
- 中文名：非線性沃爾泰拉積分方程
- 外文名：nonlinear Volterraintegral equation
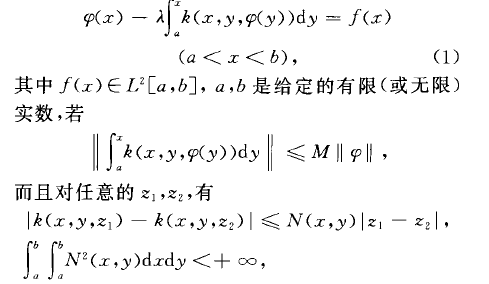
非線性沃爾泰拉積分方程（nonlinear Volterraintegral equation）積分上限變動的一類特殊的非線性方程.這指的是如下方程
非線性沃爾泰拉積分方程
這時，對任意幾，方程(1)在z,`La,b內都存在著惟一解.
非線性沃爾泰拉積分方程
相關詞條
- 非線性沃爾泰拉積分方程
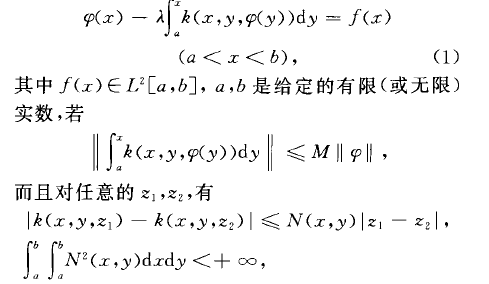
非線性沃爾泰拉積分方程是一個數學術語。非線性沃爾泰拉積分方程（nonlinear Volterraintegral equation）積分上限變動的一類特殊的非線性方程.這指的是如下方程這時，對任意幾，方程(1)在z,`...
- 非線性積分方程
非線性積分方程(nonlinear integral equation)是指不具有線性性質的一類積分方程。如果未知函式在積分號下是以非線性形式出現的，這種方程就稱為非線性積分方程。非線性積分方程也可以被分成多種類型，例如，弗雷德霍姆型、沃爾泰拉型、...
- 沃爾泰拉積分方程
是未知函式。這是沃爾泰拉（V.Volterra）在研究某個生態平衡問題時提出並討論的積分方程。弗雷德霍姆積分方程 形如 的積分方程分別稱為第一類和第二類弗雷德霍姆積分方程。其中，λ是參數，φ(x)是未知函式，。辨析 第二類沃爾泰拉積分方...
- 積分方程(數學術語)
“積分方程”一詞是 P.du B.雷蒙德於1888年首先提出的。19世紀的最後兩年，瑞典數學家（E.）I.弗雷德霍姆和義大利數學家V.沃爾泰拉開創了研究線性積分方程理論的先河。從此，積分方程理論逐漸發展成為數學的一個分支。 1899年，弗雷德...
- 洛特卡-沃爾泰拉方程
洛特卡－沃爾泰拉方程（Lotka-Volterra equations）別稱掠食者—獵物方程。由兩條一階非線性微分方程組成。經常用來描述生物系統中，掠食者與獵物進行互動時的動力學，也就是兩者族群規模的消長。此方程分別在1925年與1926年，由阿弗雷德·...
- 非線性積分運算元
如果把非線性積分方程中出現的函式看做巴拿赫空間中的元素，那么原來的積分運算就將構成一個非線性積分運算元 T 。分類 常見的非線性積分運算元有:烏雷松運算元 其中 k(x,y,t) 是 上的已知函式，它關於 t 是非線性的。沃爾泰拉運算元 ...
- 非線性方程
非線性微分方程的例子如流體力學的納維-斯托克斯方程，以及生物學的洛特卡－沃爾泰拉方程。解非線性問題最大的難處在於找出未知的解：一般來說，我們無法用已知的解來拼湊出其他滿足微分方程的未知解；而線上性的系統里，卻可以利用一組線性...
- 第三類沃爾泰拉積分方程
第三類沃爾泰拉積分方程 第三類沃爾泰拉積分方程（Volterra integral equation of the third kind）是1993年公布的數學名詞。公布時間 1993年，經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
- 比例延遲Volterra積分方程的有限元方法及加速技術
h-格式），將只增加單元個數，不增加分片多項式次數的h間斷有限元格式推廣為：增加單元個數及增加分片多項式次數並進的hp間斷有限元格式，討論了非線性光滑與弱奇異兩種形式解的延遲微分方程的hp間斷有限元方法，得到了各類h，p，hp間斷...
- 第二類弱奇異Volterra積分方程的高效數值算法
本項目擬利用插值後處理、校正、積分展開式和外推技術，提高線性及非線性弱奇異Volterra積分方程數值解的精度，並分析插值後處理在求解此類方程的優勢；將快速算法與後處理加速技術結合，套用於高維弱奇異問題，在降低計算複雜度的同時提高...
- 第二類沃爾泰拉積分方程
第二類沃爾泰拉積分方程 第二類沃爾泰拉積分方程（Volterra integral equation of the second kind）是1993年公布的數學名詞。公布時間 1993年，經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
- 第一類沃爾泰拉積分方程
第一類沃爾泰拉積分方程 第一類沃爾泰拉積分方程（Volterra integral equation of the first kind）是1993年公布的數學名詞。公布時間 1993年，經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
- 倒向隨機Volterra積分方程及其套用
在這一過程中，由Pardoux和彭實戈引入的非線性倒向隨機微分方程起到了主導作用。然而現實生活中，由於隨機微分模型在描述問題時過於理想化，故需引入更一般的隨機Volterra系統。若對其最優控制理論進行研究，則需利用倒向隨機Volterra積分方程...
- 沃爾泰拉線性積分運算元
沃爾泰拉線性積分運算元是一類重要的線性積分運算元，沃爾泰拉(Volterra,V.)於1896-1897年首先系統地研究了這一類運算元。簡介 沃爾泰拉線性積分運算元是一類重要的線性積分運算元，線性常微分方程初值問題就可以歸結為這類線性積分運算元的研究。沃爾泰拉...
- 烏雷松非線性積分運算元
烏雷松非線性積分運算元是一類很廣泛的運算元類，包含了哈默斯坦非線性積分運算元和沃爾泰拉非線性積分運算元作為特殊情況。這類運算元由於過於廣泛，研究起來困難很大，所以到目前為止，除了在該類運算元的全連續判別上有了較系統的結果之外，關於烏雷松非...
- 胡適耕
包括分歧、振動性、周期解與邊值問題，涉及非線性常微分方程、泛函微分方程、積分方程、積分微分方程及運算元方程，基於Leray-Schauder拓撲度理論，發展了多種有效的非線性分析方法，其中許多結果收集在總結性專著《非線性分析》（1996）中。
- 物理學中的數學方法
8.1 積分方程的基礎理論 8.1.1 積分方程的定義和分類 8.1.2 積分方程與微分方程的關係 8.1.3 關於齊次積分方程的理論 8.2 線性積分方程的疊代技術 8.2.1 弗雷德霍姆線性積分方程 8.2.2 沃爾泰拉線性積分方程 8.3 非線性...
- 甘四清
姚金然,甘四清,史可, 非線性沃爾泰拉延遲積分微分方程龍格-庫塔方法的散逸性, 系統仿真學報, 2009, 21(02):344-347.張浩敏，甘四清，胡琳，隨機比例方程帶線性插值的半隱式Euler方法的均方收斂性，計算數學，2009, 31(4):379-392....
