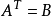相關詞條
- 轉置矩陣
將矩陣的行列互換得到的新矩陣稱為轉置矩陣,轉置矩陣的行列式不變。...... 將矩陣的行列互換得到的新矩陣稱為轉置矩陣,轉置矩陣的行列式不變。中文名 轉置矩陣 外...
- 矩陣轉置
相關概念矩陣(Matrix)本意是子宮、控制中心的母體、孕育生命的地方。在數學上,矩陣是指縱橫排列的二維數據表格,最早來自於方程組的係數及常數所構成的方陣。這一概念...
- 轉置
轉置是一個數學名詞。直觀來看,將A的所有元素繞著一條從第1行第1列元素出發的右下方45度的射線作鏡面反轉,即得到A的轉置。一個矩陣M, 把它的第一行變成第一...
- 旋轉矩陣
旋轉矩陣(英語:Rotation matrix)是在乘以一個向量的時候有改變向量的方向但不改變大小的效果並保持了手性的矩陣。旋轉矩陣不包括點反演,點反演可以改變手性,也就是...
- 矩陣(數學術語)
在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提出。矩陣是高等...
- 矩陣乘法
矩陣相乘最重要的方法是一般矩陣乘積。它只有在第一個矩陣的列數(column)和第二個矩陣的行數(row)相同時才有意義。一般單指矩陣乘積時,指的便是一般矩陣乘積。...
- 行矩陣
線上性代數中,行向量或行矩陣是1×m階矩陣,即由單行m個元素組成的矩陣,記作A=(a1 a2…am),為避免元素間的混淆,也記作A=(a1,a2,…an)。...
- 厄米特矩陣
厄米特矩陣(Hermitian Matrix,又譯作“埃爾米特矩陣”或“厄米矩陣”),指的是自共軛矩陣。矩陣中每一個第i行第j列的元素都與第j行第i列的元素的共軛相等。...
- 矩陣變換
矩陣變換是線性代數中矩陣的一種運算形式。線上性代數中,矩陣的初等變換是指以下三種變換類型 :(1) 交換矩陣的兩行(對調i,j,兩行記為ri,rj);(2) 以一個非...
- 列矩陣
列矩陣又稱列向量,是指有一列的矩陣。如果矩陣 A=(aij)m×n只有一行,即m=1,則此時稱之為行矩陣,或行向量。同樣,若 A=(aij)m×n只有一列,即n=1,這時...
- 生成矩陣
生成矩陣是線性碼的一種表示。e元[n,a]線性碼C的一個生成矩陣是有限域Fₑ上的一個a×n矩陣,其行向量構成子空間C的一組基,設C與C′是兩個e元線性碼,G...
- 矩陣範數
矩陣範數(matrix norm)是數學中矩陣論、線性代數、泛函分析等領域中常見的基本概念,是將一定的矩陣空間建立為賦范向量空間時為矩陣裝備的範數。套用中常將有限維賦...
- 埃爾米特矩陣
埃爾米特矩陣(又稱“自共軛矩陣”)是共軛對稱的方陣。埃爾米特矩陣中每一個第i 行第j 列的元素都與第j 行第i 列的元素的共軛相等。n階複方陣A的對稱單元互...
- 西爾維斯特矩陣
西爾維斯特矩陣,是與兩個多項式相關的矩陣,從這個矩陣可以知道這兩個多項式的一些信息。...
- 矩陣的秩
矩陣的秩是線性代數中的一個概念。線上性代數中,一個矩陣A的列秩是A的線性獨立的縱列的極大數。通常表示為r(A),rk(A)或rank A。線上性代數中,一個矩陣A...
- 矩陣方法
《矩陣方法》是“高等數學模組化系列教材”之一,是適合於經濟管理、理工類各專業的公共課教材。《矩陣方法》只講解矩陣的概念、矩陣的運算和矩陣的簡單套用,計畫18...
- 分解矩陣
分解矩陣(decomposition matrix)群表示論的一個特殊矩陣.即描述與各個不可約常表示相應的模表示的不可約成分重數的矩陣...
- 二維數組
二維數組本質上是以數組作為數組元素的數組,即“數組的數組”,類型說明符 數組名[常量表達式][常量表達式]。二維數組又稱為矩陣,行列數相等的矩陣稱為方陣。對稱...