相似是矩陣間的一種重要關係,在相似變換下矩陣的特徵值保持不變,相似矩陣在矩陣對角化及簡化矩陣計算方面有廣泛的套用。
基本介紹
- 中文名:矩陣相似
- 外文名:matrix similar
- 套用學科:線性代數
定義

性質
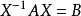



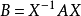




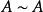
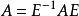
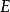



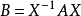



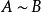
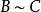

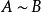
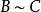


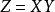


矩陣相似充分必要條件
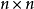

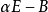
套用

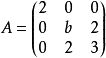
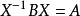





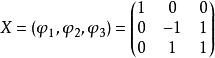
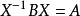

相似是矩陣間的一種重要關係,在相似變換下矩陣的特徵值保持不變,相似矩陣在矩陣對角化及簡化矩陣計算方面有廣泛的套用。

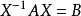



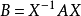




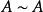
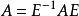
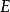



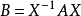



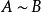
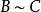

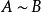
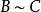


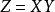


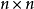

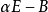

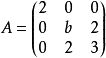
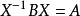





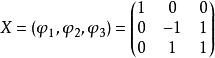
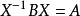

線上性代數中,相似矩陣是指存在相似關係的矩陣。設A,B為n階矩陣,如果有n階可逆矩陣P存在,使得P^(-1)AP=B則稱矩陣A與B相似,記為A~B。
相似是矩陣間的一種重要關係,在相似變換下矩陣的特徵值保持不變,相似矩陣在矩陣對角化及簡化矩陣計算方面有廣泛的套用。...
如果兩個圖形形狀相同,但大小不一定相等,那么這兩個圖形相似。...... 是相似的;反之,如果矩陣相似,那么它們可以看作是同一個線性變換在兩組不同基下對應的矩陣...
相似不變數(similarity invariant)一般指相似變換的一種特徵,即圖形經過任何相似變換都不改變的量,例如,相似比就是最基本的相似不變數。相似不變數也指相似矩陣的...
模糊矩陣(fuzzy matrix)用來表示模糊關係的矩陣,如果 集合X有m個元素,集合Y有n個元素,由集合X到集合Y中的模糊關係,可用矩陣表示。...
在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提出。矩陣是高等...
可對角化矩陣是線性代數和矩陣論中重要的一類矩陣。如果一個方塊矩陣 A 相似於對角矩陣,也就是說,如果存在一個可逆矩陣 P 使得 P −1AP 是對角矩陣,則它就...
在統計學與機率論中,自相關矩陣與自協方差矩陣,互相關矩陣與互協方差矩陣可以通過計算隨機向量(自相關或自協方差時為x,互相關或互協方差時為x,y)其第 i 個...
整數矩陣(integer matrix)是在數論中有重要套用的一種矩陣,指元素aij(i,j=1,2,…,n)都是整數的n階矩陣A=(aij),若n階整數矩陣A的行列式|A|=±1,則A稱...
線上性代數中,行向量或行矩陣是1×m階矩陣,即由單行m個元素組成的矩陣,記作A=(a1 a2…am),為避免元素間的混淆,也記作A=(a1,a2,…an)。...
相異度矩陣存儲n個對象兩兩之間的相似性,表現形式是一個n×n維的矩陣。d(i,j)是對象i和j之間相異性的量化表示,通常為非負值,兩個對象越相似或“接近”,其...
在數學中,一個距離矩陣是一個包含一組點兩兩之間距離的矩陣(即 二維數組)。因此給定N個歐幾里得空間中的點,其距離矩陣就是一個非負實數作為元素的N×N的對稱...
海森伯格矩陣是一種特殊的方陣,與三角陣很相似...... 海森伯格矩陣是一種特殊的方陣,與三角陣很相似。一個上海森伯格矩陣H的次對角元以下的所有元素都為0(hij=0,...
代數式包括有理式(整式,分式)和無理式。線上性代數中用矩陣(向量)代替代數式中的實數,得到的代數式稱為矩陣代數式。矩陣代數式遵守代數式的規律,同時具備特殊...
《矩陣分析》是2005年機械工業出版社出版的圖書,由(美)合恩(Horn.R.A.)創作,楊奇翻譯。該書是一本對數值計算研究人員來說標準的參考書。本書從數學分析的角度...
矩陣函式的概念與通常的函式概念類似,不同在於矩陣函式的自變數和因變數都是n階矩陣。矩陣函式一般用冪級數表示。矩陣函式與矩陣值函式是矩陣理論的重要內容,它們在...
當需要建立從當前矩陣到特殊類型矩陣的映射時,就用到線性運算元的矩陣(簡稱運算元矩陣)。例如從矩陣到對角矩陣的變換,用到相似變換矩陣。...
線上性代數中,矩陣的初等變換是指以下三種變換類型 :(1) 交換矩陣的兩行(對調i,j,兩行記為ri,rj);(2) 以一個非零數k乘矩陣的某一行所有元素(第i行乘以...
線上性代數和矩陣論中,有兩個m×n階矩陣A和B,如果這兩個矩陣滿足B=Q-1AP(P是n×n階可逆矩陣,Q是m×m階可逆矩陣),那么這兩個矩陣之間是等價關係。也就...
視頻矩陣是指通過陣列切換的方法將m路視頻信號任意輸出至n路監控設備上的電子裝置,一般情況下矩陣的輸入大於輸出即m>n。有一些視頻矩陣也帶有音頻切換功能,能將視頻...
