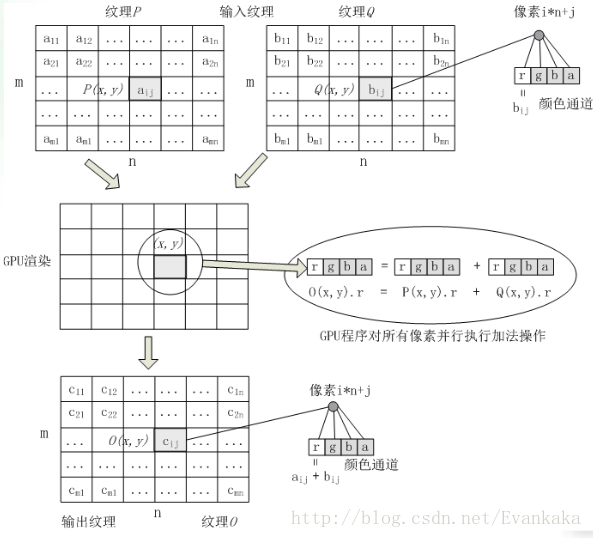
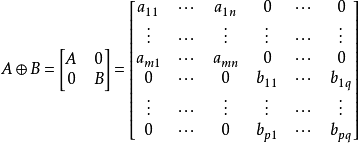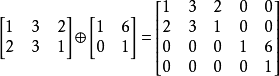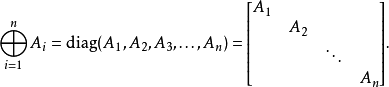矩陣加法，數學術語，定義為在數學裡，矩陣加法一般是指兩個矩陣把其相對應元素加在一起的運算。 矩陣怎么進行加減，矩陣是大學中必然要學習的一部分內容，矩陣的加減是學習矩陣的過程中最簡單的一部分。
基本介紹
- 中文名：矩陣加法
- 外文名：Matrix addition
- 特點：兩個矩陣
- 實質：其內的各元素為對應元素相加後值
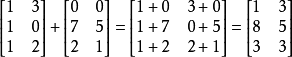
個別元素相加,做矩陣加法,直和,
個別元素相加
通常的矩陣加法被定義在兩個相同大小的矩陣。兩個m×n矩陣A和B的和，標記為A+B，一樣是個m×n矩陣，其內的各元素為其相對應元素相加後的值。例如：
也可以做矩陣的減法，只要其大小相同的話。A-B內的各元素為其相對應元素相減後的值，且此矩陣會和A、B有相同大小。例如：
做矩陣加法
一般的矩陣加（減）法如下，至於下一節的“直和”請另找參考資料。
- 先輸入要相加的兩個矩陣，大小必須一致為mxn，一般矩陣加法才有定義；
- 用滑鼠選取大小為的空白格矩陣；
- 輸入 =
- 用滑鼠選取矩陣1
- 輸入 + （若做減法則輸入 -）
- 用滑鼠選取矩陣2
7.按“Ctrl+Shift+Enter”這三個鍵的組合。
直和
另較少用來的一種運算為直和。直和可以由任何一對矩陣形成，其定義為：
舉例來說：
在任兩個向量空間內取定基底，並取兩基底的聯集為向量空間直和的基底，則兩空間上的線性變換的直和可以表成兩矩陣的直和。
一般地，n個矩陣的直和可以寫成：
