基本介紹
- 中文名:相似係數
- 外文名:similarity coefficient
- 取值範圍:(-1,1)
- 分類:關聯、距離、內積、信息、機率
簡介
選取原則
分類
關聯繫數




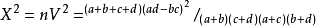
距離係數


內積係數
信息係數

屬性/樣方 | A | B | C | ||
1 | 2 | 3 | 4 | 5 | |
1 | 2 | 1 | 1 | 1 | 1 |
2 | 3 | 2 | 2 | 1 | 4 |
3 | 1 | 3 | 3 | 2 | 2 |
4 | 2 | 4 | 4 | 4 | 1 |



















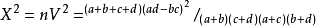



屬性/樣方 | A | B | C | ||
1 | 2 | 3 | 4 | 5 | |
1 | 2 | 1 | 1 | 1 | 1 |
2 | 3 | 2 | 2 | 1 | 4 |
3 | 1 | 3 | 3 | 2 | 2 |
4 | 2 | 4 | 4 | 4 | 1 |














相關係數是最早由統計學家卡爾·皮爾遜設計的統計指標,是研究變數之間線性相關程度的量,一般用字母 r 表示。由於研究對象的不同,相關係數有多種定義方式,較為常用...
相似係數是衡量兩個實體,或一個實體與一個實體組或兩個實體組之間相似程度的數量指標,它是進行數量分類的基礎,相似係數根據原始數據計算,實際套用時,又分相似性...
介紹 相似性係數(similarity coefficient)數量分類學術語.即以定量的形式描述分類單位之間相似性的數值,包括生物親緣關係.相似性係數數值的大小與相似性程度一致時,稱...
在對群落進行綜合中,要把特徵相似地群落資料歸併在一起,以樣地間生物種類的共同性程度來說明群落間的相似性,其數學表達式即為群落相似係數(coefficient of ...
Jaccard index, 又稱為Jaccard相似係數(Jaccard similarity coefficient)用於比較有限樣本集之間的相似性與差異性。Jaccard係數值越大,樣本相似度越高。...
相似係數就是研究樣品之間關係。...... 相似係數就是研究樣品之間關係。相似係數和距離是聚類分析中的兩個專業術語。為了將樣品(或指標,一個樣品包含n個指標,比如一...
簡單相關係數又稱皮爾遜相關係數或“皮爾遜積矩相關係數”或叫線性相關係數,是指兩個定距變數間聯繫的緊密程度。相關係數可以看作是兩個隨機變數中得到的樣本集向量...
在統計學中,皮爾遜相關係數( Pearson correlation coefficient),又稱皮爾遜積矩相關係數(Pearson product-moment correlation coefficient,簡稱 PPMCC或PCCs),是用於度量...
餘弦相似度,又稱為餘弦相似性,是通過計算兩個向量的夾角餘弦值來評估他們的相似度。餘弦相似度將向量根據坐標值,繪製到向量空間中,如最常見的二維空間。...
在統計學中,皮爾遜積矩相關係數(Pearson product-moment correlation coefficient, PPMCC)用於度量兩個變數X和Y之間的相關(線性相關),其值介於-1與1之間。在自然...
典型相關係數(canonical correlation coefficient)度量兩個隨機向量間的線性關聯程度大小的若干數量指標。 ...
相似性度量,即綜合評定兩個事物之間相近程度的一種度量。兩個事物越接近,它們的相似性度量也就越大,而兩個事物越疏遠,它們的相似性度量也就越小。相似性度量的...
Pearson相關係數(Pearson CorrelationCoefficient)是用來衡量兩個數據集合是否在一條線上面,它用來衡量定距變數間的線性關係。...
信度(Reliability)也就是可靠性,它指採用同樣的方法對同一對象重複測量時所得結果的一致性程度。信度指標通常以相關係數表示,即用同一被試樣本所得的兩組資料的...
決定係數(coefficient of determination),有的教材上翻譯為判定係數,也稱為擬合優度。是相關係數的平方。表示可根據自變數的變異來解釋因變數的變異部分。如某學生在...
相關係數是用以反映變數之間相關關係密切程度的統計指標。相關係數是按積差方法計算,同樣以兩變數與各自平均值的離差為基礎,通過兩個離差相乘來反映兩變數之間相關...
相關係數分布(distribution of correlation coeffi- cient)是樣本分布的一種。是樣本相關係數的抽樣分布。其分布形式隨總體相關係數p和樣本容量n變化而變化。...
相關係數度量指的是兩個不同事件彼此之間的相互影響程度;而自相關係數度量的是同一事件在兩個不同時期之間的相關程度,形象的講就是度量自己過去的行為對自己現在的...
相關係數法是藥用植物資源調查的方法之一。(間接觀察法)許多藥用植物其地下器官和地上器官生長存在著正相關,因此可以找出其相關係數,這樣在調查時,只調查其地上部分...
皮爾森相關係數(Pearson correlation coefficient)也稱皮爾森積矩相關係數(Pearson product-moment correlation coefficient) ,是一種線性相關係數。皮爾森相關係數是用來反映...
相似是指組成模型的每個要素必須與原型的對應要素相似,包括幾何要素和物理要素,其具體表現為由一系列物理量組成的場對應相似。對於同一個物理過程,若兩個物理現象的...
確定相關關係的存在,相關關係呈現的形態和方向,相關關係的密切程度。其主要方法是繪製相關圖表和計算相關係數。1)相關表編制相關表前首先要通過實際調查取得一系列成...
多重相關係數,亦稱復相關係數,指一個隨機變數與某一組隨機變數間線性相依性的度量。...
相關係數的檢驗(test of correlation coelli-cients)線性統計推斷中對相關係數的顯著性檢驗.從回歸直線建立的過程知道(參見“回歸直線”),對任何一組試驗觀察數據(二...
