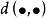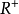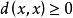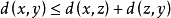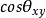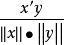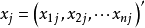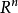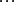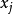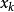相似性度量，即綜合評定兩個事物之間相近程度的一種度量。兩個事物越接近，它們的相似性度量也就越大，而兩個事物越疏遠，它們的相似性度量也就越小。相似性度量的給法種類繁多，一般根據實際問題進行選用。常用的相似性度是有：相關係數(衡量變數之間接近程度)，相似係數(衡量樣品之間接近程度)，若樣品給出的是定性數據，這時衡量樣品之間接近程度，可用樣本的匹配係數、一致度等。相似性的度量方法很多，有的用於專門領域，也有的適用於特定類型的數據，如何選擇相似性的度量方法是一個相當複雜的問題，
基本介紹
- 中文名：相似性度量
- 外文名：Similarity measurement
- 定義：綜合評定兩個事物之間相近程度
- 基礎知識：距離，相關係數
- 套用：聚類分析中
- 特殊情況：角度相似性度量
定義,基礎知識,距離,相關係數,角度,聚類分析,
定義
相似性度量，即綜合評定兩個事物之間相近程度的一種度量。兩個事物越接近，它們的相似性度量也就越大，而兩個事物越疏遠，它們的相似性度量也就越小。相似性度量的給法種類繁多，一般根據實際問題進行選用。常用的相似性度是有：相關係數(衡量變數之間接近程度)，相似係數(衡量樣品之間接近程度)，若樣品給出的是定性數據，這時衡量樣品之間接近程度，可用樣本的匹配係數、一致度等。
用數量化方法對事物進行分類，就必須用數量化方法描述事物間的相似程度。一個事物常常需要用多個變數來刻畫，如對一群用p個變數描述的樣本點進行分類，則每個樣本點可看做是p維空間的一個點，很自然的想到用距離來度量樣本點間的相似程度。
基礎知識
距離
設Ω是所有樣本點的集合，距離
是Ω×Ω→
的一個函式，滿足條件：
（1）正定性：
，x,y
Ω；d(x,x)=0，若且唯若x=0；
（2）對稱性：d(x,y)=d(y,x),x,yΩ；
（3）三角不等式：
,x,y,zΩ。
相關係數
角度
目前為止都是在用距離來度量樣本之間的相似程度，實際上在某些情況下可以採用角度相似性度量。
如果認為兩個樣本之間的相似程度只與它們之間的夾角有關，而與矢量的長度無關，那么就可以使用矢量夾角的餘弦來度量相似性。有：s(x,y)=
=
。
（1）當x與y重合時，夾角為0，相似度最大：s(x,y)=1；
（2）當x與y方向相反時，夾角為π，相似度最小：s(x,y)=-1；
聚類分析
聚類通常按照對象間的相似性進行分組，因此如何描述對象間相似性是聚類的重要問題。數據的類型不同，相似性的含義也不同。例如，對數值型數據而言，兩個對象的相似度是指它們在歐氏空間中的互相鄰近的程度；而對分類型數據來說，兩個對象的相似度是與它們取值相同的屬性的個數有關。
聚類分析按照樣本點之間的親疏遠近程度進行分類。為了使類分得合理，必須描述樣本之間的親疏遠近程度。刻畫聚類樣本點之間的親疏遠近程度主要有以下兩類函式：
（1）相似係數函式：兩個樣本點愈相似，則相似係數值愈接近1；樣本點愈不相似，則相似係數值愈 接近0。這樣就可以使用相似係數值來刻畫樣本點性質的相似性。
（2）距離函式：可以把每個樣本點看作高維空間中的一個點，進而使用某種距離來表示樣本點之間的相似性，距離較近的樣本點性質較相似，距離較遠的樣本點則差異較大。
需要由領域專家確定採用哪些指標特徵變數來精確刻畫樣本的性質，以及如何定義樣本之間的相似性測度。
