以直線為基本元素的幾何學。人們習慣於以點為幾何基本元素,而把其他幾何圖形作為點的集合。但是,也可以把其他一些幾何對象作為基本元素。例如以直線為元素就有直線幾何學,以平面上的圓或三維空間的球面作為基本元素,就有圓素或球素幾何學,等等。這樣,以點為基本元素的幾何就可以叫做點幾何學。
基本介紹
- 中文名:直線幾何
- 定義:以直線為基本元素的幾何學
- 所屬領域:幾何學
- 所屬學科:數學
簡介
直線坐標


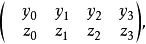




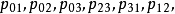









相交直線
 方程
方程線束、線把與線場
線叢、線匯與線列
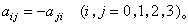 結果
結果 方程
方程用點表示直線
 線
線 條件
條件以直線為基本元素的幾何學。人們習慣於以點為幾何基本元素,而把其他幾何圖形作為點的集合。但是,也可以把其他一些幾何對象作為基本元素。例如以直線為元素就有直線幾何學,以平面上的圓或三維空間的球面作為基本元素,就有圓素或球素幾何學,等等。這樣,以點為基本元素的幾何就可以叫做點幾何學。


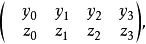




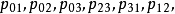









 方程
方程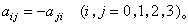 結果
結果 方程
方程 線
線 條件
條件以直線為基本元素的幾何學。人們習慣於以點為幾何基本元素,而把其他幾何圖形作為點的集合。但是,也可以把其他一些幾何對象作為基本元素。例如以直線為元素就有直線...
直線形(rectilinear figure)是一類簡單的幾何圖形,指由直線、射線、線段組成的圖形,直線形常把它所劃分的內部區域包括在內。...
從平面解析幾何的角度來看,平面上的直線就是由平面直角坐標系中的一個二元一次方程所表示的圖形。求兩條直線的交點,只需把這兩個二元一次方程聯立求解,當這個...
直線由無數個點構成。直線是面的組成成分,並繼而組成體。沒有端點,向兩端無限延長,長度無法度量。直線是軸對稱圖形。它有無數條對稱軸,其中一條是它本身,還有...
平面幾何指按照歐幾里得的《幾何原本》構造的幾何學。也稱歐幾里得幾何。平面幾何研究的是平面上的直線和二次曲線(即圓錐曲線, 就是橢圓、雙曲線和拋物線)的幾何結構...
英文Geometry一詞,是從希臘語演變而來的,其原意是土地測量、後被我國明朝的徐光啟翻譯成"幾何學"。依據大量實證研究,創造幾何學的是埃及人,幾何學因土地測量而...
歐幾里得幾何指按照古希臘數學家歐幾里得的《幾何原本》構造的幾何學。歐幾里得幾何有時單指平面上的幾何,即平面幾何。本文主要描述平面幾何。三維空間的歐幾里得幾何通常...
(幾何概念)編輯 鎖定 討論999 本詞條由“科普中國”科學百科詞條編寫與套用...除此之外,任何其他通過中點的直線都不把三角形分成面積相等的兩個部分。 [2] ...
羅巴切夫斯基幾何,也稱雙曲幾何,波利亞-羅巴切夫斯基幾何或羅氏幾何,是一種獨立於歐幾里得幾何的一種幾何公理系統。雙曲幾何的公理系統和歐氏幾何的公理系統不同之處...
直線系(system of straight lines)亦稱直線束,是具有某一共同性質的直線的集合。如在平面仿射坐標系中,與已知直線Ax+By+C=0平行的所有直線組成一個直線系,它的...
絕對幾何指滿足希爾伯特Hilbert的《幾何基礎》中的接合公理、順序公理、契約公理和連續公理等四組公理的幾何。歐式幾何就是在滿足這四組公理的基礎上還滿足平行公理,...
非歐幾里得幾何是指不同於歐幾里得幾何學的幾何體系,簡稱為非歐幾何,一般是指羅巴切夫斯基幾何(雙曲幾何)和黎曼的橢圓幾何。它們與歐氏幾何最主要的區別在於公理體系中...
斜率,亦稱“角係數”,表示一條直線相對於橫軸的傾斜程度。一條直線與某平面直角坐標系橫軸正半軸方向的夾角的正切值即該直線相對於該坐標系的斜率。 如果直線與x...
過兩點的連線即為一條直線,一般用Ax+By+C=0 (其中A、B不同時為0)來表示。...... 參考資料 1. 佚名. 空間解析幾何[M]. 科學出版社, 2004.詞條標籤: 科...
幾何定理,屬於數學領域。分為平面幾何、解析幾何。具體事例有勾股定理 餘弦定理。條目分為立體幾何,三角形的六心以及重要定理等。...
解析幾何指藉助笛卡爾坐標系,由笛卡爾、費馬等數學家創立並發展。它是利用解析式來研究幾何對象之間的關係和性質的一門幾何學分支,亦叫做坐標幾何。嚴格地講,解析...
黎曼幾何(riemannian geometry)是非歐幾何的一種,亦稱“橢圓幾何”。德國數學家黎曼,對空間與幾何的概念作了深入的研究,於1854年發表《論作為幾何學基礎的假設》一...
直線度公差指單一實際直線允許的變動全量。用於控制平面或空間直線的形狀誤差,其公差帶根據不同的情況有幾種不同的形式。...
向量幾何,於2013年2月出版。本書包含了通常在大學預科(德國九年制高中)的基礎課中有關空間向量幾何的內容,並追求下列理念: ——理論結構清晰. ——練習都附有...
17世紀晚期,在滑桿和導槽技術出現之前的一種機械設計思想。利用曲軸、連桿的結構使得一端點被限制在一條直線上運動。有各種各樣的實現方式。儘管在歷史上並沒有...
積分幾何數學中通過各種積分研究圖形性質的一門學科,本質上屬於整體微分幾何範疇。它起源於幾何機率的研究,其發展也始終與幾何機率相聯繫。積分幾何的研究從二維...
《高中幾何》是1998年中國水利水電出版社出版的圖書。...... 立體幾何部分 第一講 直線和平面 一 基本內容概述 二 基本方法與技巧 三 練習題 四 自我測驗題 第...
直線劃分平面是解析幾何研究的重要問題之一。任一直線l:Ax+By+C=0把平面內的點分成三個點的集合:(1)直線上的點的集合,點到直線的距離δ=0;(2)不包含原點...
幾何原本中的定義:當包含角的兩條線都是直線時,這個角叫做直線角。 ...... 幾何原本中的定義:當包含角的兩條線都是直線時,這個角叫做直線角。V百科往期回顧 ...
在微分幾何中, 我們希望在流形上定義一些量(標量,向量,張量等等),使得這些量和流形的局部區域坐標系的選取無關。 這樣的量就稱為幾何量。幾何量是反映物理現實...
直線射影定理(projection theorem of a right angle to a plane) 該定理是立體幾何的重要定理之一。一直角在平面上的(正)射影為 直角的充分必要條件是:原直角...
幾何,就是研究空間結構及性質的一門學科。它是數學中最基本的研究內容之一,與分析、代數等等具有同樣重要的地位,並且關係極為密切。幾何學發展歷史悠長,內容豐富。...
幾何位置線(position line)簡稱位置線。無線電導航中,通過測定無線電波傳播時間差、相位差等參數,測得方位、距離、距離差、距離和等,從而確定船艦與陸上導航電台的...
