基本介紹
基本介紹








相關概念及定理
λ截集

















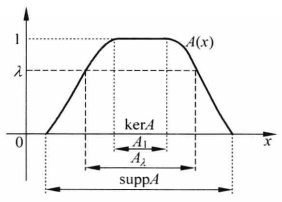
數積(截積)


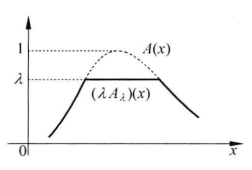
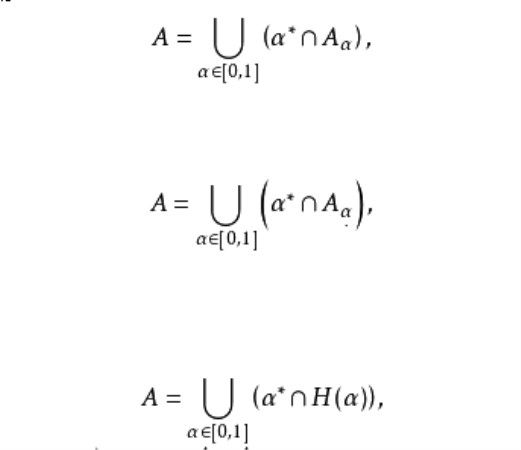





























滿足當 時,且 ,則稱N是L上的偽補。當L有偽補時,定義L模糊子集A的偽補集為 L模糊集的分解定理 如果L是完備格,仍有L模糊集的分解定理:設A是X上的L模糊集,則 其中 為A的α水平集, α*表示X上取常值α的L模糊集。
模糊集表現定理與模糊集的分解定理從不同的角度揭示了模糊集與經典集的關係,分解定理表明,任一模糊集A可由集合套 來表示;而表現定理指出,每個集合套都可以表示一個模糊集。集合套的交並補 設映射 滿足: ,則稱H為X上的一個...
2.3模糊集合的基本定理 2.3.1模糊集合的分解定理 2.3.2模糊集合的擴展原理 2.4模糊關係、模糊矩陣和模糊變換 2.4.1模糊關係及運算 2.4.2模糊矩陣 2.4.3模糊關係的合成運算及性質 2.4.4模糊變換 2.5模糊邏輯 2.5.1模糊...
兩個定理來具體實現的.通俗地講:分解定理是指任何模糊集都可分解為若干個精確集之並,而表現定理則指,一組精確集如果滿足一定條件(即構成所謂集輪),則就可表現一個模糊集,這就完全溝通了模糊集與精確集之間的關係.所以從扎德構造...
1.3模糊集合及其運算007 1.3.1模糊集合的表示方法007 1.3.2模糊集的運算009 1.3.3模糊運算元的改善011 1.4λ截集與分解定理012 1.4.1λ截集013 1.4.2分解定理014 1.5隸屬函式的確定方法017 1.5.1模糊統計方法017 1.5.2...
第2章 模糊集合 §2.1 模糊集合的概念 §2.2 模糊集的運算 §2.3 模糊集的分解定理 §2.4 模糊度與貼近度 §2.5 模糊模式識別 習題2 第3章 擴張原理與模糊數 §3.1 擴張原理 §3.2 凸模糊集與模糊數 §3.3 模糊數...
第3章 可靠性理論及模糊數學理論簡介 3.1 可靠性理論簡介 3.1.1 極限狀態方程 3.1.2 可靠指標與破壞機率 3.2 模糊集合論基礎 3.2.1 模糊集合的概念 3.2.2 模糊集合的運算定律 3.2.3 模糊集合分解定理 3.2.4 模糊數 ...
3.2模糊關係 3.2.1模糊關係的概念 3.2.2模糊關係的性質 3.2.3模糊關係的運算 3.2.4模糊關係的複合 3.2.5模糊關係的傳遞閉包 3.3模糊集的截斷與分解 3.3.1模糊集的λ截斷 3.3.2模糊集的分解定理 3.4模糊集的貼近...
第1章模糊集合及其運算 1.1經典集合與特徵函式 1.2模糊集合與隸屬函式 1.3模糊集合的運算 1.4模糊集合的分解定理與表現定理 1.5模糊性的度量 習題1 第2章模糊映射與模糊數 2.1一元模糊映射及其性質 2.2多元模糊映射及其...
1. 1 模糊集合的相關概念及其性質……… 1 1. 2 模糊集合的截集與分解定理……… 9 1. 3 模糊集隸屬函式的構造方法……… 14 1. 4 模糊關係……… 20 第2 章 模糊數……… 29 2. 1 n -維模糊數相關概念及性質...
第2章模糊集合23 2.1模糊集合概念24 2.2隸屬構造函式27 2.2.1概述27 2.2.2模糊統計27 2.2.3模糊分布29 2.3模糊集合代數運算32 2.3.1模糊集合的並、交、補運算32 2.3.2模糊集合的性質33 2.4截集35 2.5分解定理38 2...
全書共分15章,內容包括模糊集理論的三個基本概念——模糊集合、模糊關係、模糊隸屬函式;模糊集理論的三大基本原理——分解定理、表現定理和擴張原理;模糊集理論的三個基本套用——模糊聚類分析、模糊模式識別和模糊綜合評判;模糊集理論的...
1.1 模糊數學概述 1.2 模糊理論的數學基礎 一 經典集合 二 映射與擴張 三 二元關係 四 格 1.3 模糊子集及其運算 一 模糊子集的概念 二 模糊集的運算 三 模糊集的其他運算 1.4 模糊集的基本定理 一 λ-截集 二 分解定理 三...
《模糊理論及其套用》是國防科技大學出版社出版的圖書,作者是劉普寅 吳孟達 內容簡介 本書系統介紹了模糊理論的基本內容,包括模糊集及其運算、模糊性的度量、隸屬函式的確定方法、分解定理、擴展原理、表現定理,同時對模糊關係、模糊關係...
3.3.3 大規模神經網路的分解BP算法 3.3.4 模糊神經網路 3.3.5 電纜狀態預測算例 3.4 關聯矩陣模糊挖掘算法與電纜絕緣狀態分析 3.4.1 關聯分析 3.4.2 關聯矩陣挖掘算法 3.4.3 頻繁模式網路算法 3.4.4 電纜絕緣狀態...
習題1 第2章 模糊集合 2.1 模糊集合 2.1.1 模糊集合 2.1.2 模糊集合的運算 2.1.3 模糊集合的廣義運算 2.2 分解定理 2.2.1 模糊集合的λ截集 2.2.2 分解定理 2.3 隸屬函式確定的若干方法 2.3.1 模糊統計方法 2....
1.6 分解定理 1.7 集合套與表現定理 1.8 F集同構的代數系統 1.9 F集的模糊度 習題1 2 F模式識別 2.1 F集的貼近度 2.2 格貼近度 2.3 F模式識別原則 2.3.1 最大隸屬原則 2.3.2 擇近原則 2.4 幾何圖形...
《模糊數學理論及其套用》可作為高校數學專業的高年級本科生和研究生的專業課教材,也可供數學建模、災害風險分析、教育信息化綜合評價、金融工程方面的科研人員參考。圖書目錄 前言 第1章 模糊集的基本概念 第2章 模糊集的基本定理 第3...
在自己提出的區間可拓集的基礎上和多年模糊數學與水文水資源的不確定性研究基礎上建立可拓模糊集理論,包括可拓模糊集的背景研究、可拓模糊集的運算、可拓模糊集的分解定理、可拓模糊集的擴張原理與可拓模糊數、可拓模糊關係和多維可拓模糊集...
(3)作為Isbell伴隨和Kan伴隨的函子性質的特殊情形,證明了基於模糊形式概念分析和模糊粗糙集理論的概念格都是定義在由模糊形式背景和信息映射構成的範疇上的函子,並且它們都可經過模糊閉包空間分解。(4)利用Isbell伴隨建立了基於模糊集...
2.3.2模糊關係的性質 2.3.3模糊關係的複合 2.3.4模糊相似關係和等價關係 2.4賦值 2.4.1餘弦幅度法 2.4.2其他相似性方法 習題 第3章模糊向清晰的轉換 3.1模糊集的λ分割 3.2模糊關係的λ分割 3.3分解定理與表現定理 3...
2.5直覺模糊集的分解定理49 2.6直覺模糊集的真值和貼近度51 2.7直覺模糊二元關係52 習題255 第3章基於等價關係的粗糙集模型57 3.1精細集與粗糙集57 3.2上近似與下近似59 3.3知識約簡和核65 3.4相對約簡和相對核66 3.5...
第三章 模糊數學 3.1 模糊集合論的基本概念 3.1.1 經典集合論的基本概念 3.1.2 模糊集合的定義 3.1.3 模糊集合的運算 3.2 模糊集合的分解定理 3.2.1 模糊集合的截集 3.2.2 分解定理 3.3 模糊集合的隸屬度 3.3.1 ...
