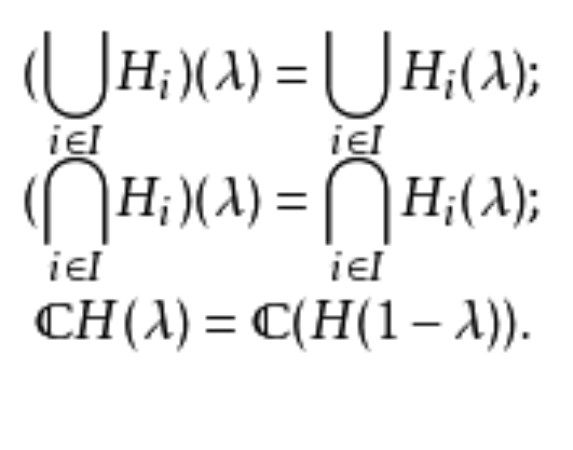模糊集表現定理(representation theorem of fuzzy sets)是模糊集合論中的一個基本定理,表現定理的意義是:X上任給一個集合套都可以拼成一個模糊集,表現定理在理論上解釋了模糊集與區間集的關係,說明模糊的對象可以由一系列賦予某種可能性度量的精確對象表述。
基本介紹
- 中文名:模糊集表現定理
- 外文名:representation theorem of fuzzy sets
- 所屬學科:數學
- 所屬問題:模糊集合論
- 簡介:模糊集合論中的一個基本定理
基本介紹

集合套的交並補






模糊集的表現定理








關於表現定理的代數說明