在數學里的範疇論中,極限的概念融貫了多種構造,包括和、積等等;範疇論中許多泛性質也可從極限來理解。
基本介紹
- 中文名:極限(範疇論)
概念介紹
余極限/上極限(colimit) | 正(向)極限(direct limit) | 歸納極限(inductive limit) |
極限(limit) | 逆(向)極限(inverse limit) | 投射極限/射影極限(projective limit) |
定義
- F:J→C.
極限
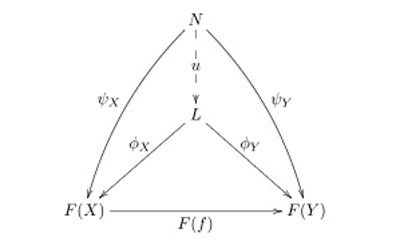
上極限
- ψX:F(X) →N
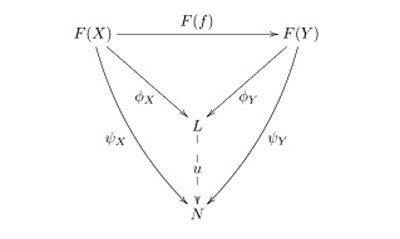
在數學里的範疇論中,極限的概念融貫了多種構造,包括和、積等等;範疇論中許多泛性質也可從極限來理解。
余極限/上極限(colimit) | 正(向)極限(direct limit) | 歸納極限(inductive limit) |
極限(limit) | 逆(向)極限(inverse limit) | 投射極限/射影極限(projective limit) |


在數學裡的範疇論中,極限的概念融貫了多種構造,包括和、積等等;範疇論中許多泛性質也可從極限來理解。...
積(範疇論)討論 編輯 積為範疇論中的一種極限。積也即C中離散子範疇的極限。積不一定存在。但若存在,則由其定義易知其在同構的意義下唯一。空積(I為空時所...
·計算機科學與技術學科研究生系列教材(中文版):高級範疇論》著重介紹範疇論的...第3章討論範疇中的各類極限,第4章討論函子與自然變換,第5章討論範疇中的“...
公共定義域的兩個態射 f : Z→ X 與g : Z→ Y 組成的圖表的余極限。...推出(範疇論)例子 編輯 這裡有一些類似範疇中推出的例子。注意每種情形,我們只...
正向極限亦稱極限,上積與推出的推廣。它是反向極限的對偶概念。在範疇論、同調代數、代數K理論、代數幾何等學科中起著重要的作用。...
保持有向上確界的函式叫做Scott連續性的或有時就叫“連續的”,如果不混淆於數學分析和拓撲學的對應概念的話。在範疇論也能找到對極限保持的術語連續。...
反向極限(inverse limit)亦稱逆向極限或上極限.它是積與拉回概念的推廣,也是正向極限的對偶概念,在範疇論、同調代數、代數K理論、代數幾何等學科中有重要套用.設矛...
在範疇論中,一個數學分支,拉回(也稱為纖維積或笛卡爾方塊)是由具有公共上域的兩個態射 f : X → Z 與 g : Y → Z 組成的圖表的極限。拉回經常寫作P...
紹了範疇論的主要內容:範疇、函子、自然變換、積與和、極限和余極限、伴隨、笛卡兒封閉的範疇和素描等,並通過很多例子.介紹了範疇論在程式設計語...
在範疇論,一個範疇C被稱為完備的,如果任何一個從小範疇到C的函子都有極限。而它被稱為上完備的,如果任何函子都有一個上極限。請查看範疇論中的極限定義。...
拉回是範疇論的基本概念之一推出的對偶概念,是一種特殊但重要的反向極限,在範疇論、同調代數、代數K理論、拓撲學與幾何等學科中有重要的套用。...
