推出 （範疇論）

在範疇論中，一個數學領域， 推出（也稱為纖維余積、纖維和、共合和或余笛卡爾方塊）是由具有公共定義域的兩個態射 f : Z → X 與 g : Z → Y 組成的圖表的余極限。

推出是拉回的範疇對偶。

基本介紹

• 中文名：推出 （範疇論）

泛性質[編輯]

明確地說，態射f與g的推出由一個對象P和兩個態射i₁:X→P與i₂:Y→P組成，使得圖表交換：

並且，推出 (P,i₁,i₂) 關於這個圖表必須是通用的。這就是說，任何其它這樣的三元組 (Q,j₁,j₂)，一定存在一個惟一的u:P→Q使得如下圖表交換：

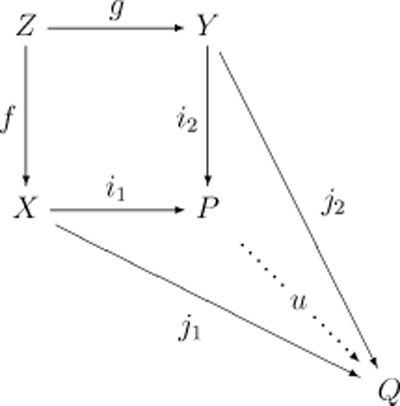
和所有泛構造一樣，推出如果存在，則在差一個同構態射的意義下是惟一的。

例子

這裡有一些類似範疇中推出的例子。注意每種情形，我們只構造推出同構類中的一個對象；如上所述，可能有其它構造方法，但是它們都是等價的。 1.假設X和Y是集合。如果我們記它們的交為Z，則由包含給出態射f:Z→X與g:Z→Y。f與g的推出是X與Y的並集附加從X和Y的包含態射。

2.黏著空間的構造是拓撲空間範疇中的推出。更準確地說，如果Z是Y的子空間且g:Z→Y是包含映射，我們可以將Y利用“黏貼映射”f:Z→X沿著Z“黏貼”到另一個空間X。黏貼空間恰好是f與g的推出。更一般地，所有黏著空間都可以這樣視為推出。

3. 上面的一個特例是楔和或一點並；這裡取X與Y為帶基點的空間而Z為 1 點空間。那么將X與Y的基點黏合起來得到的空間，便是推出。

4 在阿貝爾群範疇中，推出可以想像為“黏合直和”，以這種方式我們將黏著空間視為“黏合不交並”。零群是任何群的子群，所以任何阿貝爾群A與B，我們有同態

• f: 0 →A
  

以及

• g: 0 →B。
  

這兩個映射的推出是A與B的直和。把這種情形推廣為f與g是任何有公共定義域的同態，我們得到直和的一個商群，即模去由 (f(z),-g(z)) 組成的子群。從而我們將Z的通過f和g黏合起來了。一個類似的技巧得出任何R-模範疇中的同構。

5. 在群範疇，推出稱為共合自由積。下面在代數拓撲的塞弗特－范坎彭（Seifert-van Kampen）定理中展示出來。

性質

• 只要A∪_CB和B∪_CA存在，則存在同構態射A∪_CB≅B∪_CA。
  
• 只要推出A∪_AB存在，則存在同構態射B≅A∪_AB（這由推出的泛性質得出）。‎
  

通過余積和余等化子構造

上述所有例子都可以看成下面非常一般的構造的特例，這對只要余積和余等化子存在的任何範疇C都可行：

• 對任何C中的對象A和B，它們的余積在C中存在；
  
• 對C中的任何具有相同定義域和靶的態射j與k，j與k的余等化子在C中存在。
  

分兩步，先構造靶X與Y的余積。得到從Z到這個余積的兩個態射：從Z通過f到X，然後包含到余積；或者從Z通過g到Y，再包含到余積。f與g的推出便是這兩個新態射的余等化子。

套用：塞弗特－范坎彭定理

回到拓撲，塞弗特－范坎彭定理回答了如下問題。假設我們有一個連通空間X，被兩個連通開空間A與B覆蓋，它們的交D也是連通的（假設基點 * 在A的交中）。如果知道A,B與D的基本群，我們可以求出X的基本群嗎？答案是肯定的。

假設我們也知道包含同態π1（D,*）→π1（A，*）與π1（D，*）→π1（B，*）定理說空間X的基本群是這兩個包含映射的推出。當然，X是D到A與B的兩個包含映射的推出。從而我們可以將這個定理更深刻地理解為基本群函子保持包含推出的基本群。我們可能預計當D是單連通時最簡單，因為兩個上面同態的定義域都是平凡群。事實上確實如此，因為此時群的推出退化成自由積，即群範疇中的余積。在更一般的情形我們可以說是帶共合的自由積。

下面所列 J. P. May 的書中，在稍一般情形（覆蓋群胚）給出了詳細地說明。