拉回 （範疇論）

在範疇論中，一個數學分支，拉回（也稱為纖維積或笛卡爾方塊）是由具有公共上域的兩個態射 f : X → Z 與 g : Y → Z 組成的圖表的極限。拉回經常寫作P=X×zY.

基本介紹

• 中文名：拉回 （範疇論）

泛性質

明確地說，態射f和g的拉回由一個對象P和兩個態射p₁:P→X與p₂:P→Y組成，使得圖表

交換。並且拉回 (P,p₁,p₂) 對這個圖表必須是通用的。這便是說，任何其它這樣的三元組 (Q,q₁,q₂) 一定存在惟一的u:Q→P使得圖表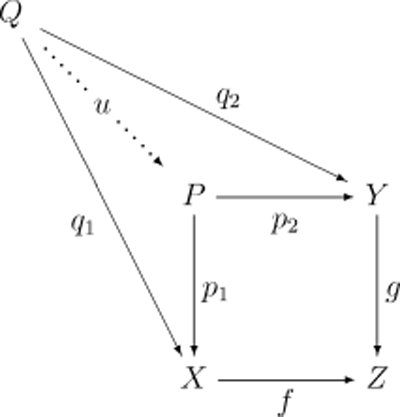

交換。和所有泛構造一樣，拉回如果存在必然在同構的意義下是惟一的。

弱拉回

一個cospanX→Z←Y的弱拉回是在 cospan 上面的錐只須滿足弱泛性質，這就是說中間映射u:Q→P不必是惟一的。

例子

在集合範疇中，f與g的拉回是集合

X×zY={(x，y)∈X×Y∣f(x)=g(y)}

以及投影映射的限制與映到X×_ZY。

• 這個例子啟發另一種方式考慮拉回：作為態射fop₁,gop₂:X×Y→Z的等化子，這裡X×Y是X和Y的二元積
  

而p₁與p₂是自然投影。這說明拉回在任何具有二元積和等化子的範疇中存在。事實上，由極限存在定理，在具有有終對象、二元積和等化子的範疇中所有有限極限存在。

拉回的另一個例子來自纖維叢理論：給定一個纖維映射 π:E→B以及一個連續映射f:X→B，拉回X×_BE是X上的纖維叢，稱為拉回叢。伴隨的交換圖表是纖維叢映射。

在任何具有終對象Z的範疇中，拉回X×_ZY恰好是普通積X×Y。

性質

• 如果X×_ZY存在，那么Y×_ZX也存在，且存在態射X×_ZYY×_ZX。
  
• 單態射在拉回下不變 ：如果箭頭f單，那么它就是箭頭p₂。例如，在集合範疇中， 如果X是Z的子集，那么對任何g:Y→Z，拉回X×_ZY是X在g下的逆像。
  
• 同構態射也不變，因此X×_XYY對任何映射Y→X成立。