範疇論中,積(或直積)的概念提取了集合的笛卡兒積、群的積、環的積、拓撲空間的積等概念的共性。本質上講,一組對象的積是到這些對象都有態射的對象中最具代表性的。
基本介紹
- 中文名:積 (範疇論)
定義
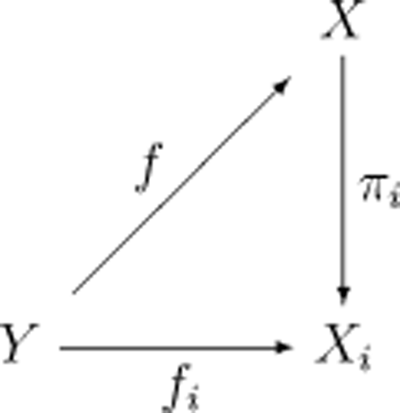

討論

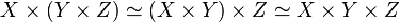
範疇論中,積(或直積)的概念提取了集合的笛卡兒積、群的積、環的積、拓撲空間的積等概念的共性。本質上講,一組對象的積是到這些對象都有態射的對象中最具代表性的。



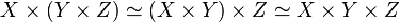
範疇論中,積(或直積)的概念提取了集合的笛卡兒積、群的積、環的積、拓撲空間的積等概念的共性。本質上講,一組對象的積是到這些對象都有態射的對象中最具代表...
積範疇(product category)是範疇論的基本概念之一。指由一些範疇組成的新範疇。...... 積範疇(product category)是範疇論的基本概念之一。指由一些範疇組成的新範疇...
上積是範疇論的基本概念之一。在範疇論中上積是積的對偶概念,是模論中直和概念的推廣,因此也稱直和或和。...
在範疇論中,一個數學領域, 推出(也稱為纖維余積、纖維和、共合和或余笛卡爾方塊)是由具有公共定義域的兩個態射 f : Z → X 與 g : Z → Y 組成的...
在數學裡的範疇論中,極限的概念融貫了多種構造,包括和、積等等;範疇論中許多泛性質也可從極限來理解。...
帶積範疇(category with product)是環上模範疇、有限生成投射模範疇等重要範疇關於直和及(交換環的情況下)張量積性質的抽象與概括。範疇是範疇論的基本概念之一。...
·計算機科學與技術學科研究生系列教材(中文版):高級範疇論》著重介紹範疇論的...第3章範疇中的極限3331等子和余等子3332積和余積3933回拉和外推46...
在哲學中,範疇(希臘語:κατηγορια)是指把事物進行歸類所依據的共同性質。比如說時間{時刻/時段},空間{距離/體積},質地{質量/密度},關係{絕對/相對}...
笛卡兒閉範疇,在範疇論中,如果任何積的態射都可通過其某個因子的態射來自然確定,那么稱該範疇具有笛卡兒閉性.此類範疇在數理邏輯和程式設計理論中尤為重要。...
在範疇論中,一個數學分支,拉回(也稱為纖維積或笛卡爾方塊)是由具有公共上域的兩個態射 f : X → Z 與 g : Y → Z 組成的圖表的極限。拉回經常寫作P...
共尾函子(final functor)是代數K理論中定義纖維範疇時用到的一類重要函子。它是一類特殊的保積函子。設(C,⊥),(D,⊥)為帶積範疇,F:C→D為保積函子。若...
