極值圖論研究圖的整體參數(如邊密度或著色數)對局部結構的影響。例如對於給定的整數r,有多少條邊可以保證n個頂點的圖無論邊怎么放置都必須包含一個K(r)完全子圖,多少條邊可以保證某種子結構出現。
基本介紹
- 中文名:極值圖論
- 外文名:Extremal graph theory
內容
歷史背景
相關定理
曼特爾定理






Turán's 定理

Erdős–Stone 定理
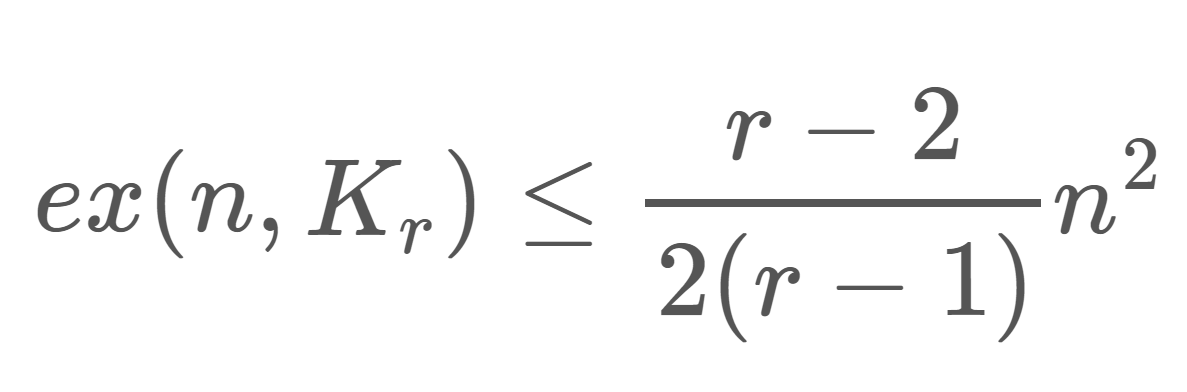

極值圖論研究圖的整體參數(如邊密度或著色數)對局部結構的影響。例如對於給定的整數r,有多少條邊可以保證n個頂點的圖無論邊怎么放置都必須包含一個K(r)完全子圖,多少條邊可以保證某種子結構出現。







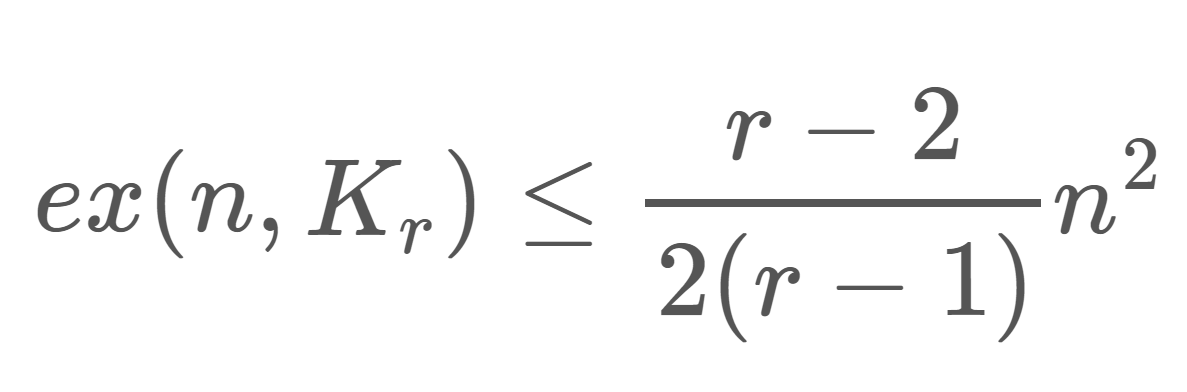
極值圖論研究圖的整體參數(如邊密度或著色數)對局部結構的影響。例如對於給定的整數r,有多少條邊可以保證n個頂點的圖無論邊怎么放置都必須包含一個K(r)完全子圖,多少條邊可以保證某種子結構出現。內容極值圖論是數學的一個分支...
《極值圖論》是依託福州大學,由范更華擔任項目負責人的重點項目。項目摘要 極值圖論研究圖的極值結構性質和極值參數等問題,包括圖論中的最佳化問題在內的很多重要問題都屬於極值圖論問題,例如特定子圖(如最長圈)的存在性、(網路)整數流...
《超圖中的一些極值問題》是依託湖南大學,由彭岳建擔任項目負責人的面上項目。中文摘要 極值圖論主要研究圖的一些不變數如邊數,色數,連通度,圖譜之間的關係,以及給出這些圖的不變數的極值使圖具有某些特定性質。1941年Turan提出了著名的...
《極值圖論中的譜圖蘭型問題》是依託天津大學,由寧博擔任項目負責人的青年科學基金項目。項目摘要 Turán型問題是極值圖論中的重要研究問題,而譜Turán型問題是經典Turán型問題的一種變形。這方面的研究主要是給出圖中各種子圖存在性的...
《極值圖論中的隨機方法》是依託同濟大學,由李雨生擔任項目負責人的面上項目。 中文摘要 一些深度的圖論極值問題,其極值圖往往超出人們的直觀想像。有時一個簡單的平均技巧可以勝過很複雜的構造。這種現象為隨機方法在圖論中套用提供了舞台...
《組合與圖論中的一類極值問題研究》是依託浙江師範大學,由張華軍擔任項目負責人的面上項目。項目摘要 極值理論是近幾十年來組合數學與圖論研究領域中一直十分活躍的一個研究方向。極值的確定以及達到極值時集族結構的確定是這一領域的主要...
《圖的譜極值理論》是依託上海師範大學,由晉亞磊擔任項目負責人的青年科學基金項目。項目摘要 圖的譜極值理論是最近十幾年興起的圖(超圖)的極值理論的一個重要研究分支,它是集代數、機率、幾何、圖論和組合等方法於一體的交叉研究...
《圖的極值能量及相關問題的研究》是依託同濟大學,由單海英擔任項目負責人的面上項目。中文摘要 圖論是現代離散數學中一個發展十分迅速的重要分支,它在化學,計算機科學,電子通訊,交通網路等方面有著重要套用。 .化學圖論是圖論與化學的...
本項目主要利用圖論的方法研究一個信道的Shannon容量、當G 和H 是一些特殊圖類時圖Ramsey數R(G,H) 的值及其上下界,R(G,H) 與Shannon容量之間的關係,圖的其他參數如獨立數、色數、譜半徑等與Shannon容量之間的關係,以及與之相關...
第7章 極值圖論 154 7.1 子圖 155 7.2 子式 160 7.3 Hadwiger猜想 163 7.4 Szemeredi正則性引理 166 7.5 正則性引理的套用 172 練習 178 註解 180 第8章 無限圖 185 8.1 基本的概念、結論和技巧 185 8.2 路、樹和...
圖論〔Graph Theory〕是數學的一個分支。它以圖為研究對象。圖論中的圖是由若干給定的點及連線兩點的線所構成的圖形,這種圖形通常用來描述某些事物之間的某種特定關係,用點代表事物,用連線兩點的線表示相應兩個事物間具有這種關係。概述...
譜極值問題是近年來圖譜理論的研究熱點。作為極值圖論的譜拓展,它主要研究圖的各種矩陣表示的極端譜參數。本項目對圖的譜極值問題開展了兩方面的深入研究。第一,基於圖的結構參數的譜極值問題:即刻畫圖的結構參數固定的圖類中譜參數的...
浙江師範大學“2018全國圖論研究生暑期學校”擬於2018年7月8日至28日開班授課,將邀請國內外知名專家學者為研究生開設“極值圖論”、“圖的染色與劃分”、“組合算法”等高質量圖論專業課程。這些課程均是圖論專業研究生的主幹課程,對其...
另外,李炯生等人研究了經典Turan數t(Kr,r,n)在可圖序列中的變形,確定了t(Kr,r,n)的度序列形式的極值å(Kr,r,n),為研究極值圖論的經典結果在可圖序列中的變形問題提供了一個範例和研究方法。張福基等人研究了譜半徑小於 ...
在本研究中所採取的方法主要為超圖方法,結構分解的技巧以及機率方法以及其他方法等,其中很多為近年來圖論與組合中新發展出來的新的理論與工具。本項目將通過對這些內容的研究,力爭在理論和方法上取得較大突破,實現擬定的目標。結題摘要...
圖譜理論是圖論中的一個重要研究領域。定向圖的斜能量的研究是該領域中的一個重要研究方向。一個定向圖的斜能量定義為它的斜鄰接矩陣的所有特徵值的模之和。定向圖的斜能量在理論化學中有著非常重要的套用。刻畫具有極值斜能量的定向圖...
江蘇師範大學全國“圖論”研究生暑期學校擬定於2016年7月10日至2016年8月31日期間開班授課,將邀請國際知名專家學者為圖論方向研究生開設《結構與極值圖論》、《Ramsey理論》、《組合算法》和《圖論與生物信息學》等高質量課程,這些課程...
極值問題 圖序列 習題 1.4 有向圖 定義和例子 頂點度 歐拉有向圖 定向和競賽圖 習題 第2章 樹和距離 2.1 基本性質 樹的性質 樹和圖中的距離 不相交生成樹(選學)習題 2.2 生成樹和枚舉 樹的枚舉 圖的生成樹 分解和...
極值組合是組合學中一個新興而熱門的學科,在今夏韓國舉行的數學家大會上有一個一小時報告和四個45分鐘報告是關於這一學科的。極值集合是極值組合中一個重要研究課題,由於它和圖論研究中的超圖理論的研究對象基本一致,所以引起了整個組合...
《圖的結構性質、參數及參數化複雜性問題研究》是依託湖北大學,由劉慧清擔任項目負責人的面上項目。項目摘要 結構圖論、極值圖論是圖論及其套用中重要的研究方向,對圖的結構問題的研究不但有重要的理論意義,而且在計算機科學、生命科學、...
《圖的匹配和染色》是依託山東大學,由王光輝擔任項目負責人的面上項目。結題摘要 圖與超圖的匹配問題是圖與組合理論中的基礎而又重要的研究方向,也是圖的因子理論,極值圖論和Ramsey理論的研究重點。圖的染色問題也是圖論中的熱門的研究...
在極值圖論領域,常常討論圖中任意兩點的內部點不相交路徑的最大數量,又記為 ,以及圖中任意兩點的邊不相交路徑的最大數量,又記為 。性質 兩條內部點不相交路徑一定是邊不相交路徑,兩條邊不相交路徑則不一定是內部點不相交路徑。...
結合極值圖論的方法,證明了當圖的獨立數為2時,Erdős-Sós猜想和Loebl-Komlós-Sós猜想成立;確定了4圈對樹的平面Ramsey數;證明了毛毛蟲的燃燒數的上界,確定了幾類特殊毛毛蟲的燃燒數。針對網路圖的結構,研究了某些具有套用背景的...
改進了Woodall的結果;運用圈結構和路系統的新的研究方法,得到了一個連通擬無爪圖包含至多k個葉子點的支撐樹或路覆蓋數至多為k-1的度和條件;結合極值圖論和代數圖論的方法,研究圖譜與圖的結構參數之間的關係,給出了判斷一個圖有...
本項目旨在運用機率方法並結合其他的一些方法,比如隨機矩陣和極值圖論中的方法,來研究隨機有向圖的規範拉普拉斯特徵值問題,隨機圖的完全二部圖劃分問題以及相對應的隨機超圖的劃分問題。這些問題的探討將會豐富隨機圖論的研究。結題摘要 圖...
基於距離的拓撲指標是圖的重要不變數之一,在化學圖論中有著重要而廣泛的套用。本項目中,我們主要研究基於距離的拓撲指標,包括的極值問題,這類指標與圖的其他不變數的內在關係等,基於頂點度的不變數(特定條件下也屬於距離不變數)的...
