基本介紹
- 中文名:一元二次方程的根的分布
- 外文名:Distribution of roots of a quadratic equation of one variable
實根分布
區間與區間根
















分布討論


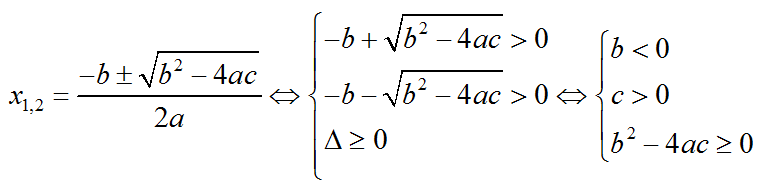
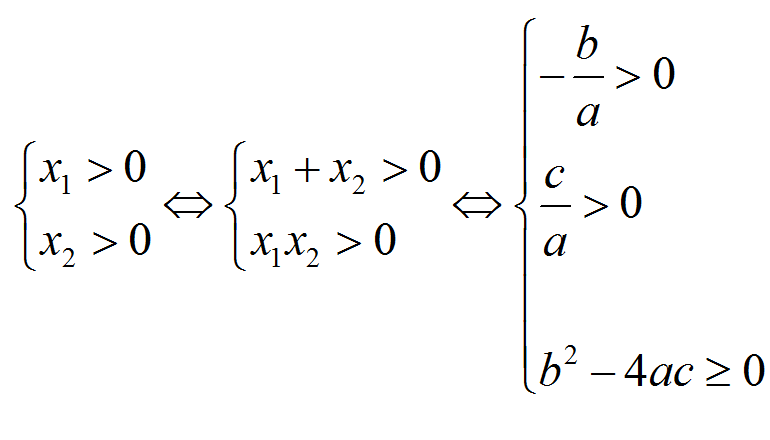

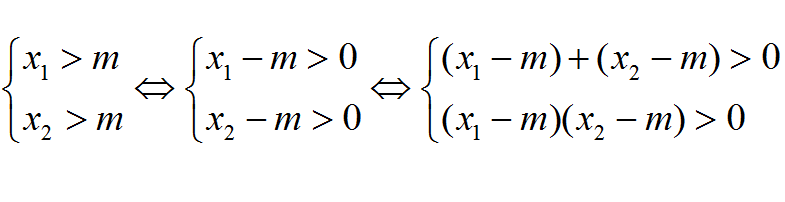
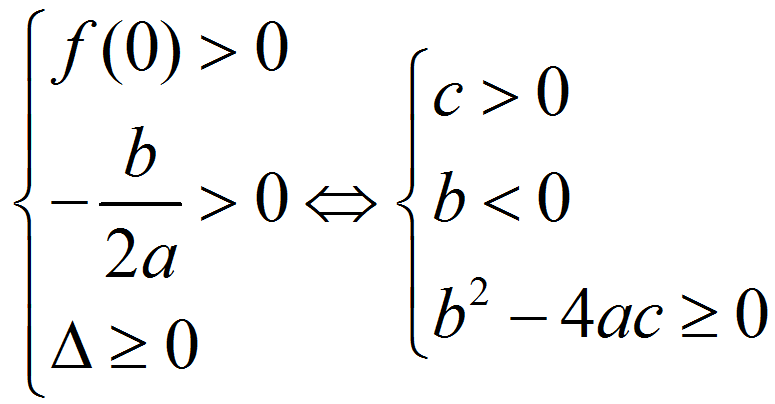





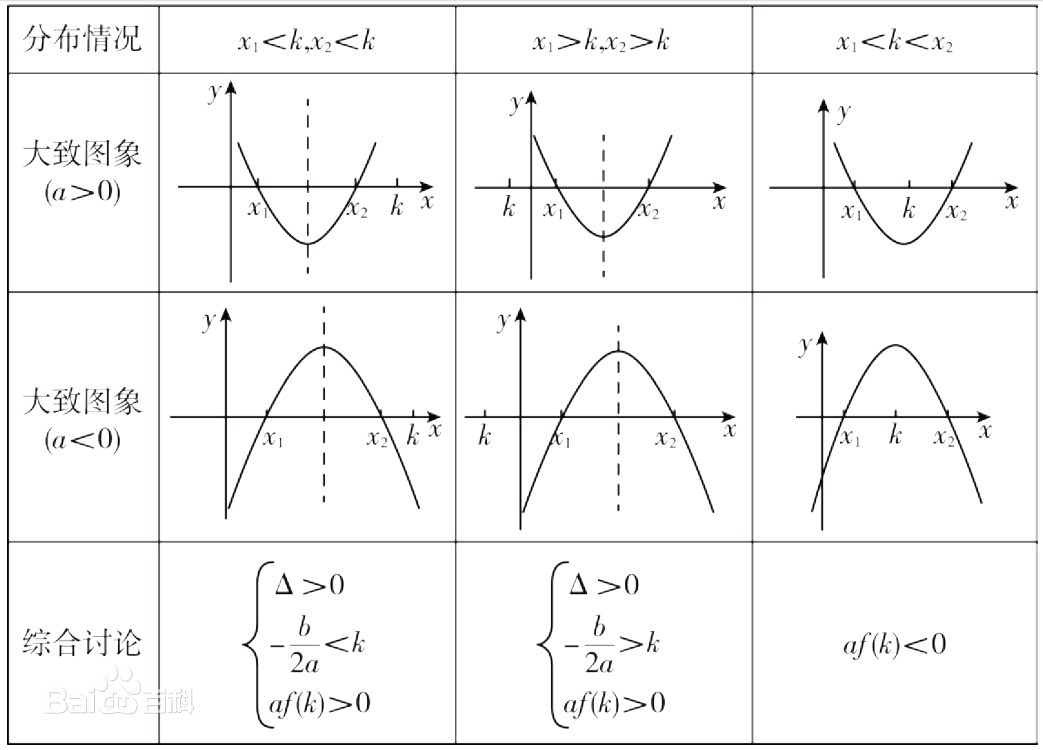
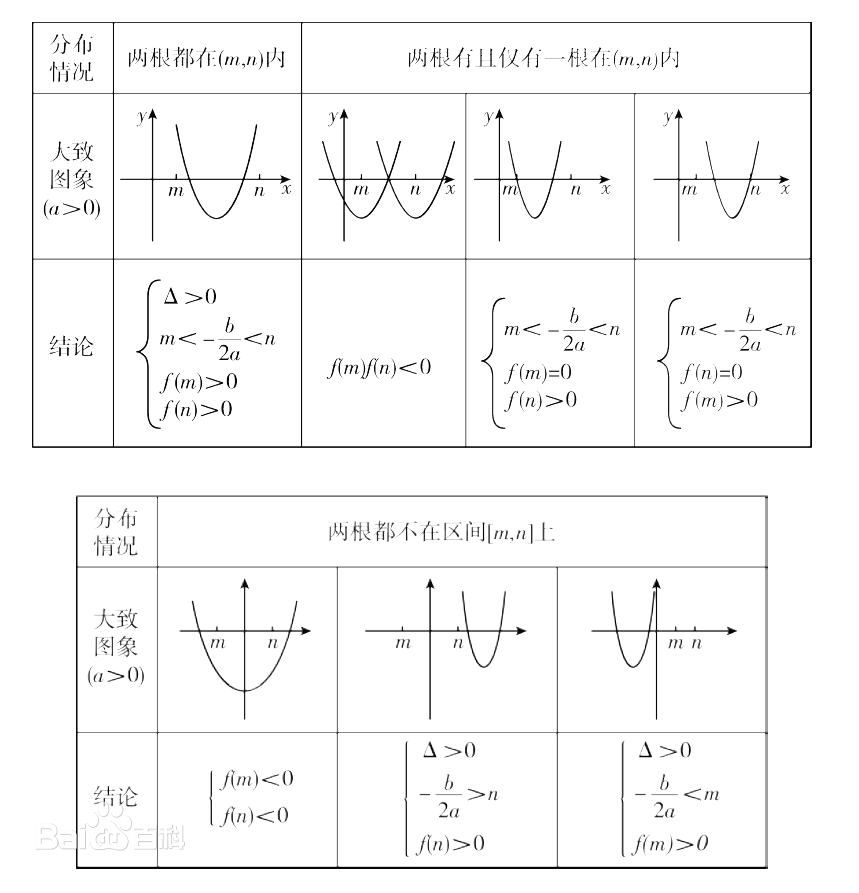
常見問題


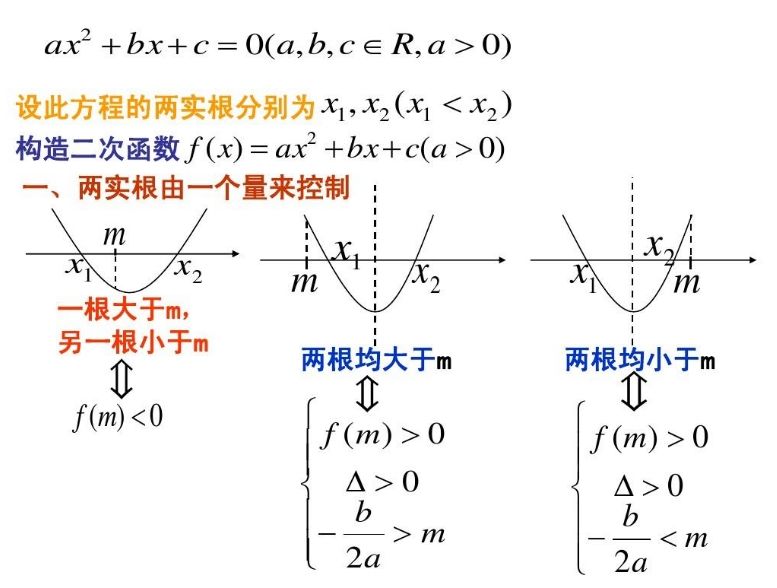
根的分布一般指本詞條


















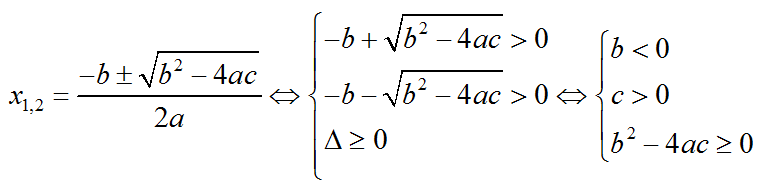
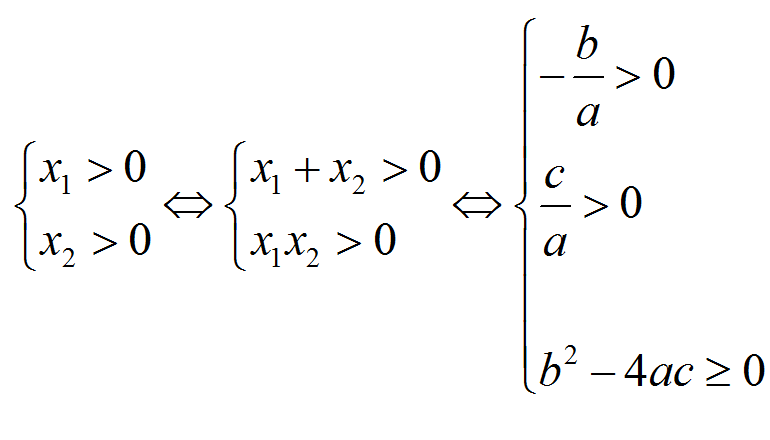

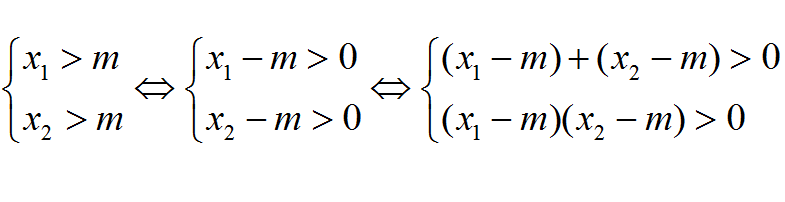

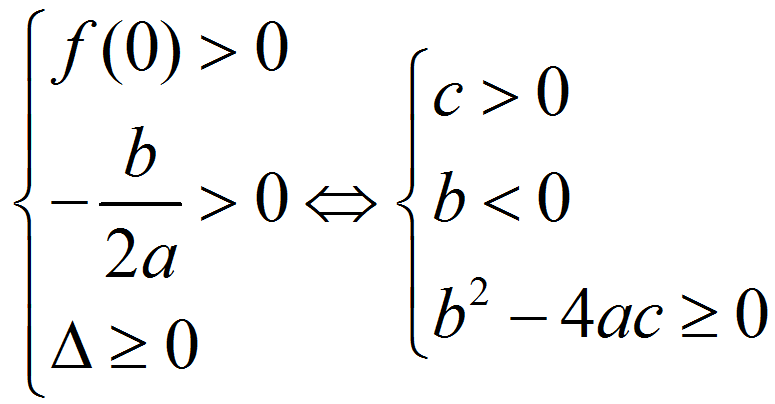









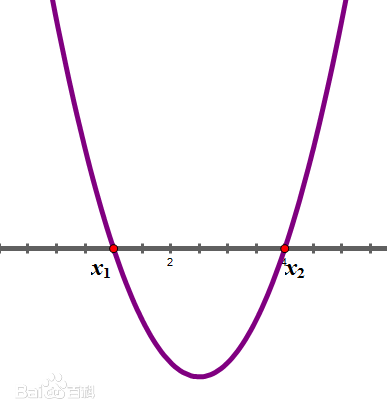
根的分布一般指一元二次方程實根分布問題,是一類通過題乾中根的分布確定一元二次函式參數取值範圍的問題.根的分布是國中數學一元二次函式的基礎內容.一元二次方程的根實質上對應二次函式圖象與 x 軸的交點橫坐標.因此,二次方程的...
棉根的次生韌皮部分布多酚色素腺,其顏色與根皮近似,因此在外觀上不易發現。棉根中棉酚的含量隨生育進程不斷增加。木栓形成層 棉根的次生維管組織形成後,中柱鞘細胞進行徑向分裂,其外層形成木栓形成層。該形成層向外產生排列緊密的...
形成層向內分化次生木質部,向外分布次生韌皮部,同時分化射線薄壁細胞。初生木質部被次生木質部包圍在中央;而初生韌皮部則被擠壓、壓扁、退化消失。肉質根的次生生長使蘿蔔的中柱部分逐漸膨大,而初生皮層和表皮(根被皮)不能相應膨大,...
依根系在土壤中的分布與生長方式,可分為水平根和垂直根。與地面近於平行生長的根系稱為水平根,與地面近於垂直生長的根係為垂直根。根系分類 植物根的總合稱為根系(root system),分為直根系(taproot system)和鬚根系(fibrous root ...
時,根據平方根的意義,方程(I)有兩個不等的實數根 ⑵當 時,方程(I)有兩個相等的實數根 ;⑶當 時,因為對任意的實數 ,都有 ,所以方程(I)無實數根。但是方程(I)在複數域內有解 ,配方法 一般地,如果一個一元...
一般土質疏鬆、肥力較高的農田,作物根系活動層的深度大於土壤密實、肥力較低的農田;深根作物的作物根系活動層比淺根作物深。據測定,冬小麥根深可達1.5~2.0m以上,但90%的根量分布在0~60cm表土層內;玉米根系最深可達到2m...
分布 生長於林內或灌木叢中。廣布於長江流域以南省區,北至西北地區。採制 根全年可采,洗淨,曬乾或鮮用。果實於8~10月果熟時採摘。成分 果實含維生素C0.016%~0.2%,成熟果實含獼猴桃甙(actinidine)。葉含槲皮素(quercetin)...
排根,是指在側根上形成的似毛刷狀密集而有限生長的一組根簇。起源於中柱鞘細胞,具有嚴密的時空發育規律。形成機制 環境條件會影響根系在土壤中的分布。如在缺磷條件下,本來是深根植物的大豆,其磷高效品種會將大量基部根系分布在...
牛蒡根,中藥名。為菊科植物牛蒡Arctium lappa L.的根。牛蒡分布於東北、西北、中南、西南及河北、山西、山東、江蘇、安徽、浙江、江西、廣西等地。具有散風熱,消毒腫之功效。常用於風熱感冒,頭痛,咳嗽,熱毒面腫,咽喉腫痛,齒齦腫痛...
根冠還與根的向地性生長有關。根冠細胞中常含有澱粉體,且多集中分布在細胞下方。一些水生植物和對重力不敏感的攀援植物根冠細胞中往往沒有澱粉體。因此多數人認為,細胞中澱粉體的分布可能與根的向地生長有一定的關係。澱粉體有平衡石...
3.在受累神經根前根分布區域內,呈現不同程度的下運動神經元性癱瘓:肌力減退,肌肉萎縮,腱反射減退或消失等。如頸胸神經根炎症狀多發生於肩胛帶和上肢;腰骶神經根炎症狀則見於下肢,骶神經根損害較重時尚有失張力性膀胱和性功能障礙...
禾草類與其他單子葉植物則具有鬚根系統,其特徵是一群根的直徑大約相等;此根絡非由主根分枝生成,而是包含從莖的基部長出且大量分枝的根。分布情況 根系在土壤中的分布是非常廣泛的。在良好的土壤條件下,種子萌發後不久,其根系的拓展...
山胡椒根,中藥名。為樟科山胡椒屬植物山胡椒Lindera glauca(Sieb.et Zucc.)Bl的根。植物山胡椒,分布於中國山東、安徽、浙江、江西、福建、台灣、河南、湖南、廣東、廣西、四川、雲南等地。具有祛風通絡,理氣活血,利濕消腫,化痰止咳...
根群(radical grow p)一種由升列定義的廣義可解群.若群G具有因子為冪零群的一個升列,則稱G為根群.根群類是很有用的廣義可解群類,因為它包含所有的可解群和所有的局部冪零群,而且它具有比局部可解群類好得多的性質.根...
根系構型是模擬根系在土壤中的根系空間分布的情況,根據空間維數分為二維構型和三維構型。現在研究根系構型,主要是為了仿真出根系在不同的生長條件下的分布情況,從而得出更加有利於生產和實驗的品種或者根繫結構。可以更好的利用土壤的營養...
主要分布於亞洲熱帶地區,國內見於雲南省東南部、海南省五指山山區、台灣南部和廣西壯族自治區十萬大山山區的熱帶溝谷中。分布範圍 熱帶雨林中具有板根的樹木十分普遍,使這種“板根現象”成為其重要特徵之一。在我國雲南孟定溝谷中的雨林,具...
