基本介紹
- 中文名:柯西-黎曼方程
- 外文名:Cauchy-Riemann Equations
- 屬性:偏微分方程
- 學科:數理
- 簡稱:C-R方程
- 發明者:柯西
- 發展者:黎曼
研究歷史
方程
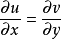

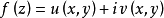

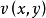

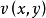
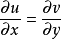

證明過程
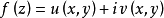
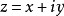
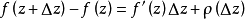
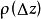
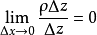
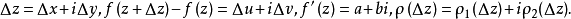
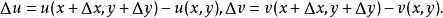
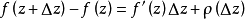
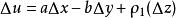

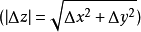
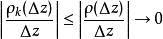
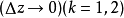

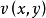
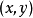
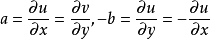
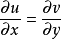

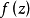

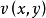
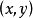
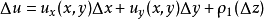
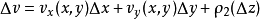
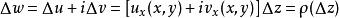
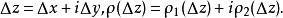
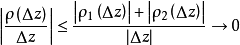
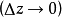
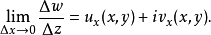
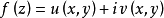
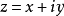
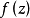
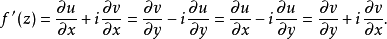

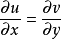

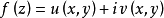

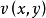

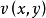
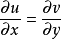

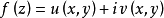
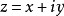
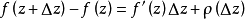
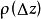
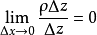
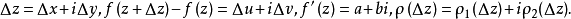
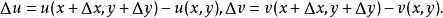
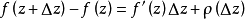
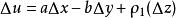

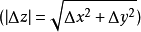
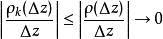
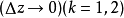

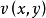
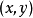
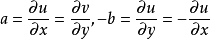
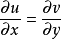

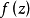

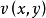
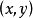
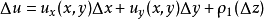
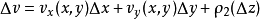
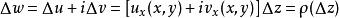
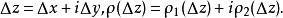
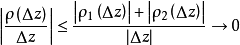
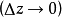
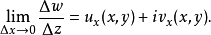
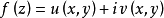
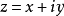
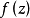
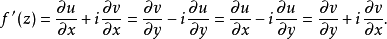
柯西--黎曼微分方程是提供了可微函式在開集中為全純函式的充要條件的兩個偏微分方程,以柯西和黎曼得名。這個方程組最初出現在達朗貝爾的著作中。後來歐拉將此方程...
柯西-黎曼條件,即柯西--黎曼微分方程,提供了可微函式在開集中為全純函式的充要條件的兩個偏微分方程,以柯西和黎曼得名。這個方程組最初出現在達朗貝爾的著作中。...
得到了現在所稱的柯西一黎曼方程組,歐拉得出了理想流體動力學方程組。18世紀末,蒙日(Monge )開創了用幾何解釋偏微分方程的思想,對一階和二階非線性方程建立了...
存在,且在D內除去一個勒貝格測度為零的集合外,柯西一黎曼方程成立,則f=a+iv在D內全純. 柯西(Cauchy,A. -I_.)最初於1814年給出解析函式的定義時,要求導...
他的名字出現在黎曼ζ函式,黎曼積分,黎曼引理,黎曼流形,黎曼空間,黎曼映照定理,黎曼-希爾伯特問題,柯西-黎曼方程,黎曼思路迴環矩陣中。 [1] ...
在這個理論中,王見定大膽地將“柯西-黎曼”方程組的兩個方程式分開,將滿足其中任一個方程式的函式定義為半解析函式,從而實現了對解析函式的推廣,為研究解析函式所不...
B.黎曼從這一定義出發對複函數的微分作了深入的研究,後來,就把上述的偏微分方程組稱為柯西-黎曼方程,或柯西-黎曼條件。參考資料 1. 《數學辭海》總編輯委員會....
根據柯西-黎曼方程,一個全純函式的共軛函式所對應的向量場的旋度是0。曲線積分套用簡介 在各種保守力的場都是路徑無關的,一個常見的例子就是重力場或電場。在...
處存在連續偏導數,並且滿足柯西-黎曼方程(或稱柯西-黎曼條件):這個條件有時簡稱C-R條件或稱達朗貝爾-歐拉條件。函式f(z)在區域D內解析的第四個等價條件是莫雷拉...
B.黎曼從這一定義出發對複函數的微分作了深入的研究,後來,就把上述的偏微分方程組稱為柯西-黎曼方程,或柯西-黎曼條件。參考資料 1. 《數學辭海》總編輯委員會....
到了十九世紀,上述兩個方程在柯西和黎曼研究流體力學時,作了更詳細的研究,所以這兩個方程也被叫做“柯西-黎曼條件”。複變函數論的全面發展是在十九世紀,就像微...
1.解析函式的概念與柯西—黎曼方程2.初等解析函式3.初等多值函式第二章習題第三章複變函數的積分1.復積分的概念及其簡單性質2.柯西積分定理...
人們期望與柯西解析函式的定義相等價的定義,即用柯西-黎曼方程定義的解析性能有相應的改進。1923年,羅曼(Looman,H.)給出了上述更廣的定理,但他的證明有缺陷。...
B.黎曼從這一定義出發對複函數的微分作了深入的研究,後來,就把上述的偏微分方程組稱為柯西-黎曼方程,或柯西-黎曼條件。林德勒夫漸近定理函式極限 編輯 函式極限是...
B.黎曼從這一定義出發對複函數的微分作了深入的研究,後來,就把上述的偏微分方程組稱為柯西-黎曼方程,或柯西-黎曼條件。參考資料 1. 《數學辭海》總編輯委員會....
§1.解析函式的概念與柯西-黎曼方程1.複變函數的導數與微分2.解析函式及其簡單性質3.柯西-黎曼方程§2.初等解析函式1.指數函式2.三角函式與雙曲函式...
B.黎曼從這一定義出發對複函數的微分作了深入的研究,後來,就把上述的偏微分方程組稱為柯西-黎曼方程,或柯西-黎曼條件。參考資料 1. 《數學辭海》總編輯委員會....
以複數為係數的二元不可約多項式構成的方程P(z,w)=0所確定的(多值)解析函式...的每一個點z=x+iy處存在連續偏導數,並且滿足柯西-黎曼方程(或稱柯西-黎曼...
