基本介紹
- 中文名:柯西-黎曼條件
- 外文名:Cauchy–Riemann equations
- 屬性:偏微分方程
簡介
研究歷史
方程
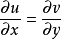
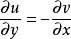
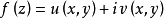




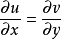
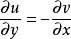
證明過程
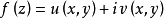
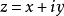
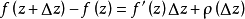

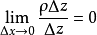
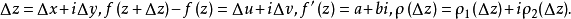
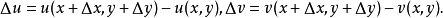
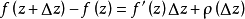
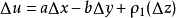
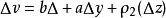





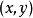
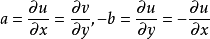
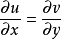
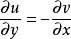
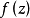


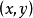
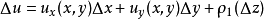
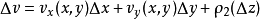

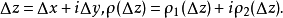
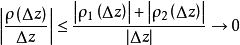
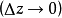
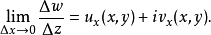
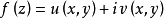
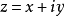

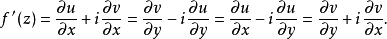
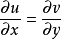
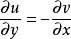
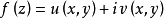




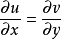
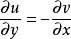
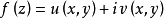
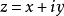
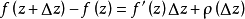

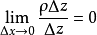
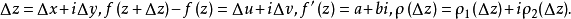
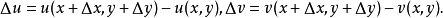
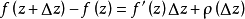
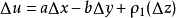
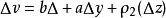





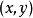
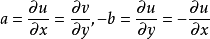
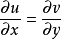
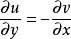
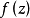


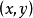
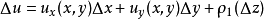
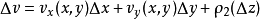

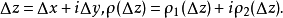
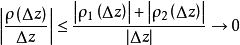
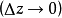
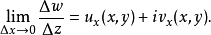
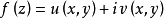
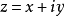

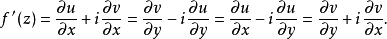
柯西-黎曼條件,即柯西--黎曼微分方程,提供了可微函式在開集中為全純函式的充要條件的兩個偏微分方程,以柯西和黎曼得名。這個方程組最初出現在達朗貝爾的著作中。...
黎曼(德,1826-1866年):幾何觀點,黎曼面。1851年博士論文《單複變函數一般理論...此外,建立了柯西-黎曼條件,真正使這方程成為複分析大廈的基石,揭示出複函數與實...
一般邊界條件有三種形式,分為本質邊界條件(狄里克雷邊界條件)、自然邊界條件(黎曼邊界條件)、混合邊界條件(柯西邊界條件)。對於自然邊界條件,一般在積分表達式中可...
柯西--黎曼微分方程是提供了可微函式在開集中為全純函式的充要條件的兩個偏微分方程,以柯西和黎曼得名。這個方程組最初出現在達朗貝爾的著作中。後來歐拉將此方程...
協調條件是保證連續固體變形後仍保持其整體性和連續性的條件。這些條件可用固體內...右柯西-格林變形張量的協調條件為其中 表示第二類克里斯托費爾符號, 則表示黎曼-...
微分方程求解中的邊界條件有三類基本形式:本質邊界條件(狄里克雷邊界條件)、自然邊界條件(黎曼邊界條件)、混合邊界條件(柯西邊界條件)。...
王見定發現,儘管解析函式已形成比較完善的理論並得到多方面的套用,但自然界能夠滿足“柯西-黎曼”方程組條件的現象很少,使解析函式的套用受到較大的限制。由此,尋找...
在二維問題中,定義一個函式 (稱為復勢)的充要條件是 和 為調和函式及滿足柯西-黎曼方程。複函數定義為:式中 及 。在複平面 中, 和 形成一個矩形坐標網路。...
處存在連續偏導數,並且滿足柯西-黎曼方程(或稱柯西-黎曼條件):這個條件有時簡稱C-R條件或稱達朗貝爾-歐拉條件,函式f(z)在區域D內解析的第四個等價條件是莫雷拉定...
到了十九世紀,上述兩個方程在柯西和黎曼研究流體力學時,作了更詳細的研究,所以這兩個方程也被叫做“柯西-黎曼條件”。複變函數論的全面發展是在十九世紀,就像微...
儘管解析函式已形成比較完善的理論並得到多方面的套用,但自然界能夠滿足“柯西-黎曼”方程組條件的現象很少,使解析函式的套用受到較大的限制。由此,尋找把“柯西-...
在D內解析的另一個等價條件是: 在D內的每一個點 處存在連續偏導數,並且滿足柯西-黎曼方程(或稱柯西-黎曼條件):這個條件有時簡稱C-R條件或稱達朗貝爾-歐拉條件...
B.黎曼從這一定義出發對複函數的微分作了深入的研究,後來,就把上述的偏微分方程組稱為柯西-黎曼方程,或柯西-黎曼條件。參考資料 1. 《數學辭海》總編輯委員會....
在柯西的定義中,首先出現了自變數一詞,同時指出對函式來說不一定要有解析表達式。不過他仍然認為函式關係可以用多個解析式來表示,這是一個很大的局限。1822年傅里...
B.黎曼從這一定義出發對複函數的微分作了深入的研究,後來,就把上述的偏微分方程組稱為柯西-黎曼方程,或柯西-黎曼條件。參考資料 1. 《數學辭海》總編輯委員會....
解析函式的概念及柯西-黎曼條件 §2.1.1 導數與微分 §2.1.2 柯西一黎曼條件 §2.1.3 解析函式的定義 第二節 解析函式與調和函式的關係 §2.2.1 共軛...
B.黎曼從這一定義出發對複函數的微分作了深入的研究,後來,就把上述的偏微分方程組稱為柯西-黎曼方程,或柯西-黎曼條件。參考資料 1. 《數學辭海》總編輯委員會....
x,y),z=x+iy在D內解析的另一個等價條件是:u=u(x,y),v=v(x,y)在D內的每一個點z=x+iy處存在連續偏導數,並且滿足柯西-黎曼方程(或稱柯西-黎曼條件...
B.黎曼從這一定義出發對複函數的微分作了深入的研究,後來,就把上述的偏微分方程組稱為柯西-黎曼方程,或柯西-黎曼條件。 S類意義 編輯 20世紀初,在對單位圓盤...
