基本介紹
- 中文名:有理分式域
- 外文名:field of rational fractions
- 所屬學科:數學
- 所屬領域:初等代數
- 相關概念:有理分式、多項式等
定義


有理分式




有理分式的運算
有理分式的加法






有理分式的乘法





有理分式的減法





有理分式的除法



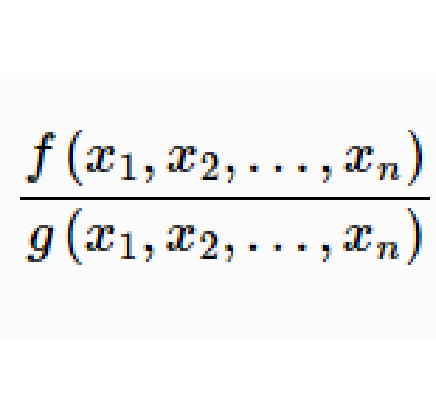

























有理分式域(field of rational fractions)是包含多元多項式環的最小域。數域P上全體有理分式,稱為數域P上的有理分式域,記為P(x)。...
有理函式域(rational function field)是一種重要的純超越擴張。純超越擴張是一類重要的超越擴張。設擴域K在F上的超越基為S,若K=F(S),則稱此域擴張為純超越...
在抽象代數中,分式環或分式域是包含一個整環的最小域,典型的例子是有理數域之於整數環。此外分式環也可以推廣到一般的交換環,此時通常稱作全分式環。 分式環有...
的有限擴張也稱為代數數域,在代數數論有重要地位。有理數的另一個擴張域是關於...它們構成一個域,記作K(X),是多項式環K[X]的分式域。它是域K的擴域,次數...
,tn)是K上t1,…,tn的有理分式域,多項式f(x)=x-t1x+t2x-…+(-1)tn∈F[x]稱為K上n次一般方程,設K是一個特徵為0的域,則K上n次一般方程在F=K(t1...
p進數是數論中的概念,也稱作局部數域,是有理數域拓展成的完備數域的一種。p進數的概念首先由庫爾特·亨澤爾於1897年構思並刻畫,其發展動機主要是試圖將冪級數...
亦稱分式理想,是理想概念的推廣。設R為一整環,K為其商域(分式域),M K是R模。若存在非0的c∈R使cM={cm|m∈M} R,則稱M為分式理想。通常的理想(又稱...
設a為複數,若存在係數為有理整數的首一(即最高次項係數為1)多項式f(x)使f...所有整數全體構成一個交換環I,其商域(或稱分式域)即為代數數全體構成的域A。...
,tn)是K上t1,…,tn的有理分式域,多項式f(x)=x-t1x+t2x-…+(-1)tn∈F[x]稱為K上n次一般方程,設K是一個特徵為0的域,則K上n次一般方程在F=K(t1...
從代數的觀點來看,如果D是一個連通集,則亞純函式的集合是全純函式的整域的分式域。這和有理數Q和整數Z的關係類似。半純函式定義擴展 編輯 在數學中,黎曼曲面...
的觀點來看,如果D是一個連通集,則亞純函式的集合是全純函式的整域的分式域。...比如有理函式就是在擴充複平面上的亞純函式,它是兩個多項式的商而Q(z)的...
