映射在一點處微分(differential of map at apoint)亦稱映射在一點處的切映射一種特殊的映射.由微分流形之間的可微映射誘導出的它們切空間之間的一種線性映射.若M,N分別是m維，n維微分流形，f : M->N是可微映射，則按下述方式f誘導出切空間T pM到Tf}p,N的線性映射
f稱為可微映射f在pEM處的微分f.若f是微分同胚映射，則對於p<M,f,，是同構.
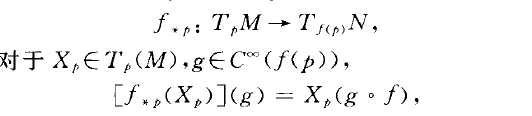
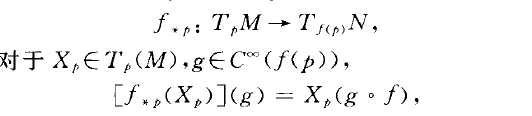
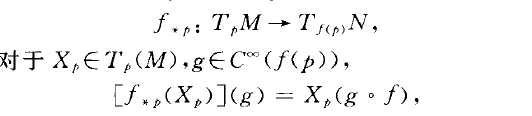
映射在一點處微分(differential of map at apoint)亦稱映射在一點處的切映射一種特殊的映射.由微分流形之間的可微映射誘導出的它們切空間之間的一種線性映射.若...
光滑映射在一點穩定性(stability of asmooth mapping at a point)是指光滑映射在一點局部經小擾動後本質不變的特性。光滑映射是一類連續映射,是微分拓撲學的基本...
如果說微分是導數的一種推廣,那么微分形式則是對於微分函式的再推廣。微分函式對每個點 給出一個近似描述函式性質的線性映射 ,而微分形式對區域 內的每一點給出...
映射到變化量的線性部分的線性映射。這個映射也被稱為切映射。給定的函式在一點的微分如果存在,就一定是唯一的。在數學中,微分是對函式的局部變化率的一種線性...
微分形式的一個優點就是能做外微分 運算。 比如 是一個r次微分形式, 那么 。這就把一個r次微分形式映到了r+1次微分形式。換言之,我們有映射d: → . ...
微分流形可微映射 設φ是從C流形M到C流形N的連續映射,如果對於N上的任意Cr函式ƒ,M上的函式ƒ。φ總是Cr的,則稱φ是Cr可微映射,或簡稱Cr映射。如果φ...
映射正則點(regular point of map)微分流形上一類特殊的點.指微分流形上的那種點,可微映射在該點處是淹沒映射。...
設D是Rn中的一個區域,f:D→Rn是以D為定義域的映射,如果f在D上的每一點處可微,則稱f為D上的可微映射。...
微分在數學中的定義:由函式B=f(A),得到A、B兩個數集,在A中當dx靠近自己時,函式在dx處的極限叫作函式在dx處的微分,微分的中心思想是無窮分割。微分是函式改...
切映射是一種可微映射。微分流形之間的可微映射誘導出它們的切叢之間可微映射。...... 切映射是一種可微映射。微分流形之間的可微映射誘導出它們的切叢之間可...
正則映射擴展——映射正則點 編輯 映射正則點(regular point of map):微分流形上一類特殊的點,指微分流形上的那種點,可微映射在該點處是淹沒映射。...
3.1映射分析中的微分長度比59 3.1.1迴轉曲面的微分長度比60 3.1.2特殊方向的長度比61 3.2Γ曲線為經線時的可展切曲面62 3.2.1可展切柱面的表達62 3.2.2...
擬共形映射,又稱擬保角映射,原本是複分析中的一套技術手段,現已發展為一套獨立學科。該理論在橢圓型偏微分方程中占有重要地位。這一理論在研究有理函式的疊代、...
研究微分流形和可微映射的一個數學分支。微分流形除了是拓撲流形外,還有一個微分結構。因此,對於從一個微分流形到另一個微分流形的映射,不僅可以談論它是否為...
G)為X,且對任何x∈X都有惟一的y∈Y滿足G(x,y),則稱G為從X到Y的映射...複流形和實流形概念的引進擴大了微分幾何和實分析的對象,產生了像大範圍分析...
向量叢是流形切叢概念的抽象和推廣,它是微分拓撲學和代數拓撲學的重要研究對象。映射亦稱函式。數學的基本概念之一。也是一種特殊的關係。設G是從X到Y的關係,G...
。這個映射也被稱為切映射。給定的函式在一點的微分如果存在,就一定是唯一的。在數學中,微分是對函式的局部變化率的一種線性描述。微分可以近似地描述當函式自變數...
一般的流形概念,起始於對於可微流形的研究,在點集拓撲中已經熟悉把一元或多元連續函式的概念,推廣為拓撲空間之間連續映射的概念。 切空間是微分流形在一點處所...
n維微分流形 M 上一個開集U到切叢T(M)到映射X,若df∘X=X,則稱 X 為關於 f 的不變向量場。...
所有滿足以上條件的微分同胚映射全體集合,在等價意義下構成的群稱作n條弦生成辮群, 其中的元素稱作辮。辮群還可以用另一方式定義。 考慮平面上n個不同點組成的無...
《複變函數引論》以真解析函式為主線安排了複數與擴充複平面、複變函數與解析函式、複變函數沿有向曲線的積分、級數、奇點與留數、共形映射共6章內容,從微分、...
這時φt:U→φt(U)是C微分同胚。對於局部單參數變換群{φt}及U中的任一點p,由t→φt(p)定義的映射γp:Iε→M是M中過p的一條參數曲線。它稱為群{...