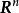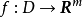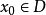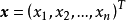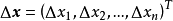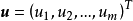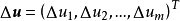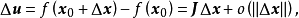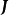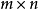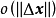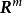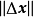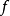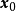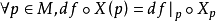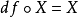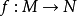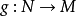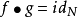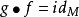n維微分流形 M 上一個開集U到切叢T(M)到映射X,若df∘X=X,則稱 X 為關於 f 的不變向量場。
基本介紹
- 中文名:不變矢量場
- 外文名:invariant vector field
- 適用範圍:數理科學
簡介,向量場,定義,微分同胚,可微映射,
簡介
向量場
向量場是切叢的截面。
n維微分流形 M 上一個開集U到切叢T(M)到映射X,即 X:U→T(M),且滿足 ,特別取 U為M時,稱X為M上的向量場。
,特別取 U為M時,稱X為M上的向量場。

若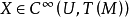 ,則稱向量場 X 為光滑向量場。
,則稱向量場 X 為光滑向量場。
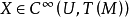
定義
微分同胚
在數學中,微分同胚是適用於微分流形範疇的同構概念。這是從微分流形之間的可逆映射,使得此映射及其逆映射均為光滑(即無窮可微)的。
若在微分流形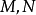 之間存在微分同胚映射,則稱
之間存在微分同胚映射,則稱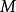 與
與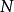 是微分同胚的。
是微分同胚的。
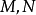
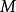
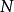
可微映射
設D是Rn中的一個區域,f:D→Rn是以D為定義域的映射,如果f在D上的每一點處可微,則稱f為D上的可微映射。
設D是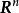 中的一個區域,
中的一個區域,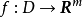 是以D為定義域的映射,
是以D為定義域的映射,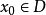 ,如果對於自變數
,如果對於自變數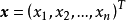 的增量
的增量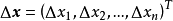 ,因變數
,因變數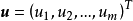 的增量
的增量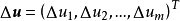 可以分解為
可以分解為