基本域

數學上，給出一個拓撲空間和在其上作用的群，一個點在群作用下的像是這個作用的一個軌道。一個基本域是這個空間的一個子集，包含了每個軌道中恰好一點。基本域具體地用幾何表現出抽象的軌道代表集。

構造基本域的方法有很多。一般會要求基本域是連通的，又對其邊界加上一些限制，例如是光滑或是多面的。基本域在群作用下的像，就會把空間密鋪。

基本介紹

• 中文名：基本域
• 外文名：Fundamental domain
• 領域：數學
• 適用領域：拓撲學
• 定義：數學上，給出一個拓撲空間和在其上作用的群，一個點在群作用下的像是這個作用的一個軌道

簡介

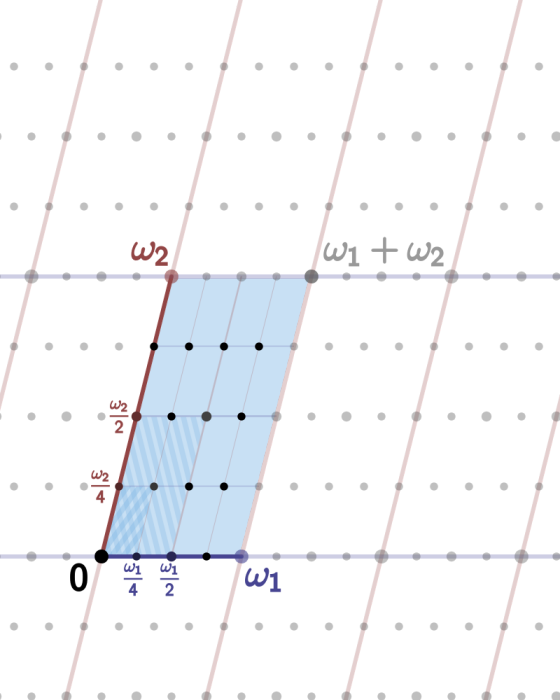
構造基本域的方法有很多。一般會要求基本域是連通的，又對其邊界加上一些限制，例如是光滑或是多面的。基本域在群作用下的像，就會把空間密鋪。

拓撲空間

拓撲空間是一種數學結構，可以在上頭形式化地定義出如收斂、連通、連續等概念。拓撲空間在現代數學的各個分支都有套用，是一個居於中心地位的、統一性的概念。拓撲空間有獨立研究的價值，研究拓撲空間的數學分支稱為拓撲學。

定義

拓撲空間是一個集合和其上定義的拓撲結構組成的二元組。的元素通常稱為拓撲空間的點。而拓撲結構一詞涵蓋了開集，閉集，鄰域，開核，閉包，導集，濾子等若干概念。從這些概念出發，可以給拓撲空間作出若干種等價的定義。在教科書中最常見的定義是從開集開始的。 

開集公理

的子集族稱為開集系（其中的元素稱為開集），若且唯若其滿足如下開集公理：

O₁：，。

O₂：若（），則（對任意並運算封閉）。

O₃：若，則。（對有限交運算封閉）。

從開集出發定義其它各概念：

從開集定義閉集：的子集是閉集，若且唯若是開集。

從開集定義鄰域：的子集是點的鄰域，若且唯若存在開集，使。

從開集定義開核：的子集的開核等於包含的所有開集之並。

閉集公理

的子集族稱為閉集系（其中的元素稱為閉集），若且唯若其滿足如下閉集公理：

C₁：，。

C₂：若（），則（對任意交運算封閉）。

C₃：若，則。（對有限並運算封閉）。

（顯然，閉集是開集的對偶概念）。

從閉集出發定義其它各概念：

從閉集定義開集：的子集是開集，若且唯若是閉集。

從閉集定義閉包：的子集的閉包等於包含A的所有閉集之交。

拓撲之間的關係

同一個全集可以擁有不同的拓撲，有些是有用的，有些是平庸的，這些拓撲之間可以形成一種偏序關係。當拓撲的每一個開集都是拓撲的開集時，稱拓撲比拓撲更細，或稱拓撲比拓撲更粗。

僅依賴於特定開集的存在而成立的結論，在更細的拓撲上依然成立；類似的，僅依賴於特定集合不是開集而成立的結論，在更粗的拓撲上也依然成立。

最粗的拓撲是由空集和全集兩個元素構成的拓撲，最細的拓撲是離散拓撲，這兩個拓撲都是平庸的。

群

在數學中，群是一種代數結構，由一個集合以及一個二元運算所組成。

一個群必須滿足一些被稱為“群公理”的條件，也就是封閉性、結合律、單位元和對於集合中所有元素存在逆元素。很多熟知的數學結構比如數系統都遵從這些公理，例如整數配備上加法運算就形成一個群。如果將群公理的公式從具體的群和其運算中抽象出來，就使得人們可以用靈活的方式來處理起源於抽象代數或其他許多數學分支的實體，而同時保留對象的本質結構性質。

群在數學內外各個領域中是無處不在的，這使得它們成為當代數學的組成的中心原理。

群與對稱概念共有基礎根源。對稱群把幾何物體的如此描述物體的對稱特徵：它是保持物體不變的變換的集合。這種對稱群，特別是連續李群，在很多學術學科中扮演重要角色。例如，矩陣群可以用來理解在狹義相對論底層的基本物理定律和在分子化學中的對稱現象。

群的概念引發自多項式方程的研究，由埃瓦里斯特·伽羅瓦在1830年代開創。在得到來自其他領域如數論和幾何學的貢獻之後，群概念在1870年左右形成並牢固建立。現代群論是非常活躍的數學學科，它以自己的方式研究群。為了探索群，數學家發明了各種概念來把群分解成更小的、更好理解的部分，比如子群、商群和單群。除了它們的抽象性質，群理論家還從理論和計算兩種角度來研究具體表示群的各種方式（群的表示）。對有限群已經發展出了特別豐富的理論，這在1983年完成的有限簡單群分類中達到頂峰。從1980年代中葉以來，將有限生成群作為幾何對象來研究的幾何群論，成為了群論中一個特別活躍的分支。

密鋪

密鋪（Tessellation）或稱平面填充、細分曲面（subdivision surface），是指把一些較小的表面填滿一個較大的表面而不留任何空隙。在數學上，密鋪可以推廣到更高的維度，稱為空間填充。

圖1.馬拉喀什的瓷磚

有規律的密鋪具有周期性的重複模式，較特殊的種類有平面正密鋪由正多邊形組成，而且是由同一種形狀獨立完成整個密鋪，和平面半正密鋪與擬半正密鋪用不只一個正多邊形完成密鋪，前者在每個角落都有相同配置，後者則是周期性的重複模式。有規律的密鋪形成的圖案可分為17組。缺乏重複圖案的密鋪被稱為“非周期密鋪”。非周期性平鋪使用一些較小的表面填滿一個較大的表面而不留任何空隙，但由於每一片的形狀皆不相同，以致無法形成重複圖案。有時可用在面積上計算圖案的大小。