基本介紹
基本例子
典型群
有限群
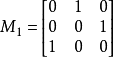
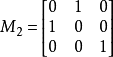
表示論
例子
- 李群列表(en:table of Lie groups),有限單群列表(list of finite simple groups),以及單李群列表(list of simple Lie groups)中有許多例子。
- 參見傳遞有限群列表(list of transitive finite linear groups)

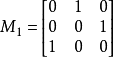
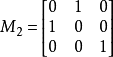
在數學中,一個矩陣群(matrix group)G 由某個域 K(通常為了方便是固定的)上可逆方塊矩陣組成,群運算分別為矩陣乘法與逆運算。更一般地,我們可考慮一個交換環 R...
《矩陣群——李群理論基礎》是2009年清華大學出版社出版的圖書,作者是Baker,Andrew。本書介紹了李群和李代數基礎理論,內容先進,講述方法科學,易於掌握和使用。...
在V 上取一組基,把線性變換 ρ(g) 在此基下的矩陣記作 T(g),則 g→ T(g) 是 G 到一般線性群 GL(n,K) 內的同態,它稱為 G 的矩陣表示。...
《Springer大學數學圖書·矩陣群:李群理論基礎》是一本(美國)貝克(Andrew Baker))編制,由清華大學出版社在2009年11月1日出版的書籍。...
群表示論用具體的線性群(矩陣群)來描述群的理論,是研究群的最有力的工具之一。在19世紀末和20世紀初它由F.G.弗羅貝尼烏斯和W.伯恩賽德獨立開創,而弗羅貝...
k2群是(K2-group)代數K理論中的一類重要的群...... }定義群的滿同態}p:ST(R)}E(R),其中成表(i}j)位置a的初等矩陣(參見“施坦貝格群”、“懷特海群”)...
群表示論就是用具體的線性群(矩陣群)來描述群的理論.其核心是群特徵標理論。弗羅貝尼烏斯發表的與這一論題相聯繫的論文有“群特徵標”(ber die Gruppen...
1.7 傳遞辛矩陣群二 不同時間的有限元離散2.1 雙曲型偏微分方程的特徵線理論概要2.2 波動方程2.3 變動邊界問題與混和元2.4 剛性雙曲型偏微分方程例題2.5 ...
泛代數是以一般代數系統為研究對象的一個數學分支。在諸如矩陣群、置換群、變換群等具體的群概念基礎上,經過抽象概括而得出抽象群的概念,與此類似,可以在一般的群...
