基本介紹
- 中文名:嚴格單調函式
- 外文名:strictly monotonic function
定義










性質

定理
定理 1






定理 2





定理 3








推論 1





注















































增函式和減函式統稱為單調函式,嚴格增函式和嚴格減函式統稱為嚴格單調函式。定義設 為定義在 上的函式.。 若對於任何 ,當 時,總有(i) ,則稱 為 上的增函式,特別當成立嚴格不等式 時,稱 為 上的嚴格增函式;(ii)...
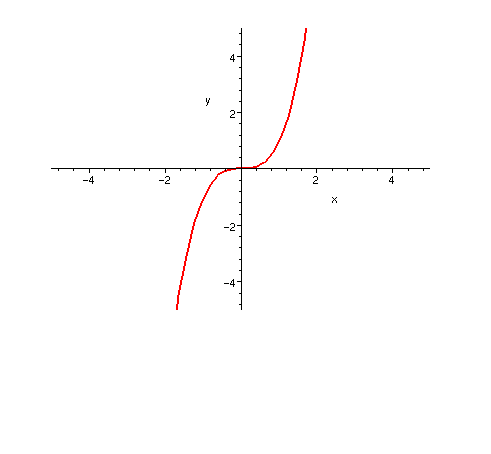
一個嚴格遞增的連續函式,它不處處可微。下面的例子是由Pringsheim作出的,令 易見, 在 上連續,因為當x≠0時, 所以 在 和 內都是嚴格遞增的,又當x>0時, ,而當x ,可見 在 內也是嚴格遞增的,但由於 不存在,因而 在x=0處不可微。注意:有人或許會猜測,嚴格單調函式的不可微的點都...
反函式存在定理 定理:嚴格單調函式必定有嚴格單調的反函式,並且二者單調性相同。在證明這個定理之前先介紹函式的嚴格單調性。設y=f(x)的定義域為D,值域為f(D)。如果對D中任意兩點x₁和x₂,當x₁ 證明:設f在D上嚴格單增,對任一y∈f(D),有x∈D使f(x)=y。而由於f的嚴格單增性,對D中任一...
在這一區間具有(嚴格的)單調性,這一區間叫做y= 的單調區間,在單調區間上增函式的函式圖像是上升的,減函式的函式圖像是下降的。注意 函式的單調性也叫函式的增減性;函式的單調性是對某個區間而言的,它是一個局部概念;判定方法 判定函式在某個區間上的單調性的方法步驟有兩種主要方法:定義法 設任意x1、x...
單調區間是指函式在某一區間內的函式值y,隨自變數x的值增大而增大(或減小)恆成立。性質 若函式y=f(x)在某個區間是增函式或減函式,則就說函式在這一區間具有(嚴格的)單調性,這一區間叫做函式的單調區間。此時也說函式是這一區間上的單調函式。註:在單調性中有如下性質。圖例:↑(增函式)↓(減函式...
單調數列(Monotone sequence of numbers)是一類重要的數列。單調數列有:(遞)增數列,(遞)減數列,嚴格增數列,嚴格減數列。也有人把它們分別稱作不減、不增、增、減數列。嚴格增數列與嚴格減數列合稱嚴格單調數列。單調數列也就是定義在自然數集上的單調函式。上述定義與把單調函式的定義用於數列所得到的結果是...
證明:嚴格單調函式必定有嚴格單調反函式,並且單調性相同(證法參考反函式詞條),因此只要證明反函式也在其定義域上連續即可。設f是定義在D上的嚴格單增的函式(嚴格單減同理)。作輔助函式g(x)=x,顯然g(x)的反函式就是它本身。由於g(x)在R上是連續的,因此它在D上也是連續的。①若D是開區間,設x...
羅巴切夫斯基函式(Lobachevskian function)簡稱羅氏函式,羅氏幾何中的重要函式關係。在羅氏平面上,若∠BAP是線段AB的平行角,d(AB)=x,μ(∠BAP)=α,則函式:α=π(x)稱為羅巴切夫斯基函式。羅巴切夫斯基函式是嚴格單調遞減的連續函式。這個函式可以用初等函式表示如下:π(x)=2arccot e,其中ρ為曲率半徑。定義...
sigmoid函式也叫Logistic函式,用於隱層神經元輸出,取值範圍為(0,1),它可以將一個實數映射到(0,1)的區間,可以用來做二分類。在特徵相差比較複雜或是相差不是特別大時效果比較好。Sigmoid函式為神經網路中的激勵函式,是一種光滑且嚴格單調的飽和函式,其表達式為:該飽和函式的上、下界為(0,1)。具有以下優...
如果一個數列從第二項起每一項都小於它前面的一項,那么這個數列就叫作嚴格遞減數列。基本介紹 一個實數列{aₙ},如果從第二項起,每一項都不大於它的前一項,即有 這樣的實數列叫遞減數列,也叫下降數列,或說這一數列單調下降,例如,數列0.1,0.01,0.001,0.0001.…和數列2,1,0,-1,-2,…...
《函式單調性》是開封市十七中提供的微課課程,主講教師是孫月欣。課程簡介 從國中所學的函式圖像上升或下降的趨勢引出函式單調性及單調區間,再根據知識擴充使學生理解函式單調性必須有嚴格的代數定義,從而引出定義,師生共同理解定義,並著重講解定義中的“任意”。最後通過一道練習題,幫助學生掌握一個函式具有多個增...
單調映射(monotone mapping)首先由穆爾於1925年在連續統上定義,懷伯恩於1934年引入了單調映射類。概念 單調遞增一元函式概念在對偶作用意義下的無窮維推廣,設 是巴拿赫空間, 為 的對偶空間, ⊂ , ,若有 則稱 為單調映射。若上式子中的等號僅當 時成立,則稱 為嚴格單調映射。若存在連續函式 ...
(-∞,0)∪(0,+∞),μ=α(為整數),當α是奇數時為(-∞,+∞),當α是偶數時為(0,+∞),μ=p/q,p,q互素,作為複合函式進行討論。②指數函式: (a>0 ,a≠1),定義域為( -∞,+∞),值域為(0,+∞),a>1 時是嚴格單調增加的函式( 即當x2>x1時,y2>y1),0 和y=log(x)的圖形...
單調遞增函式,數學術語,一般地,設函式f(x)的定義域為I:如果對於定義域I內某個區間D上的任意兩個自變數的值x₁,x₂,當x₁ 注意 1、函式的單調性也叫函式的增減性;2、函式的單調性是對某個區間而言的,它是一個局部概念;3、判定函式在某個區間上的單調性的方法步驟有兩種主要方法:求解方法 1)...
《函式的單調性》是壽光市第一中學提供的微課課程,主講教師是宋天梅。課程簡介 通過生活中的事例引入,並通過熟悉的函式類型引出函式的單調性,給出函式的單調性的定義,通過定義進行聯繫,熟悉並且學會套用,給出相應的變換,和作業。進一步對單調性定義的深入理解。知識點 高中 數學 二.函式/4.函式的單調性 ...
嚴格凹函式的性質 1)一元可微函式在某個區間上是嚴格凹的,若且唯若它的導數在該區間上嚴格單調減的。2)一元連續可微函式在區間上是嚴格凹的,若且唯若函式位於所有它的切線的下方:對於區間內的所有 和 ,都有 。特別地,如果 ,那么c是 的最大值。3)一元二階可微的函式在區間上是嚴格凹的,當且...
如果{xₙ}中只有有限項相等,即數列從某項開始嚴格單調遞增,那么因為{xₙ}有上界,可取所有{xₙ}的上界組成一個數集B,並取A=R/B。則:①由取法可知數集B非空,而{xₙ}為嚴格單調遞增數列,故 。∴ 。② 。③∵A中任何元素都不是{xₙ}的上界,∴ 。又∵B中任何元素都是{xₙ}的...
嚴格單調(把被積函式條件加強了,所以叫加強條件下的積分中值定理),則在積分區間 上至少存在一個點 ,使得下式成立:定理證明 不妨假設 是嚴格遞減函式,如圖1所示。顯然有 ;即 ...(1)根據基本版本的積分中值定理我們知道 至少存在一點 ,使得 ...(2)將(2)式代入(1)式可以得到:由於b>a,上式除以...
strictly monotonic function 嚴格單調函式 ; 嚴格單彈數 strictly convex function [數] 嚴格凸函式 ; 凸函式 ; 狹義凸函式 strictly speaking 嚴格地說;嚴格來說 strictly confidential 絕密;極機密 strictly prohibit 嚴禁 雙語例句 1This is not strictly true.這不完全正確。《牛津詞典》2The industry is ...
例13 設f(n)是定義在自然數集上且取自然數值的嚴格單調遞增函式,f(2)=2,當m,n互質時,有f(mn)=f(m)f(n),求證:對一切自然數n,有f(n)=n。(六)幾個例題 例14 已知 , ,…, 與 , ,…, 是2n個數,且 2+ 2+…+ 2=1, 2+ 2+…+ 2=1,求證: , ,…, 中存在一個值...
這一限制條件時也是成立的。雖然該定理通常是以分母bₙ為正數數列的情形加以敘述的,但注意到該定理對分子aₙ的正負沒有限制,所以原則上把對數列bₙ的限制條件替換為“嚴格單調遞減且趨於負無窮大”也是沒有問題的。與洛必達法則的疊代用法類似,在嘗試套用斯托爾茲-切薩羅定理考察數列的極限時,如果發現兩個...
3、抽樣特性曲線是一條嚴格單調下降的函式曲線,即對於p1L(p2)。曲線與參數 由於OC曲線與抽樣方案是一一對應的,所以改變方案中的參數必然導致OC曲線發生變化,但是如何變化呢?它們之間的變化有什麼關係?下面分三種情況進行分析:1、保持n固定不變,令c變化,則如果c增大,則曲線向上變化,方案放寬;如果c減小,...
指數函式 y=ax(a>0 ,a≠1),定義成為(-∞,+∞),值域為(0 ,+∞),a>0 時是嚴格單調增加的函式(即當x2>x1時,) ,00), 稱a為底 , 定義域為(0,+∞),值域為(-∞,+∞)。a>1 時是嚴格單調增加的,0 以10為底的對數稱為常用對數 ,簡記為lgx。在科學技術中普遍使用的是...
正(負)向曲線常以Γ(Γ)表示.設φ,ψ是曲線Γ的等價參數表示,即存在嚴格單調連續函式f,使ψ=φ°f,則當f嚴格增時稱f保持定向,這時Γ用φ,ψ表示的始點與終點一致。當f嚴格減時稱f反轉定向。對平面簡單閉曲線,通常按下列方法規定其正、負向:設曲線Γ在xy平面上,z軸與x,y軸形成右手坐標系,構想...
