加強條件的積分中值定理

積分中值定理分為積分第一中值定理和積分第二中值定理，它們各包含兩個公式。積分中值定理揭示了一種將積分化為函式值， 或者是將複雜函式的積分化為簡單函式的積分的方法， 是數學分析的基本定理和重要手段， 在求極限、判定某些性質點、估計積分值等方面套用廣泛。但是其閉區間的鬆弛，導致在其閉區間端點處點的討論存在限制，這裡將討論加強條件的積分中值定理，將其區間加強為開區間。

簡介

基本版本的積分中值定理如下：

若函式在閉區間連續，則在積分區間上至少存在一個點，使下式成立：

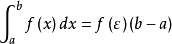
現在加強條件的積分中值定理如下：

若函式在閉區間嚴格單調（把被積函式條件加強了，所以叫加強條件下的積分中值定理），則在積分區間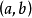上至少存在一個點，使得下式成立：

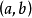
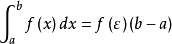
定理證明

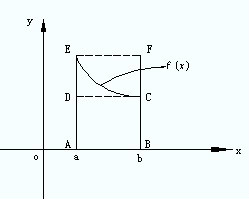
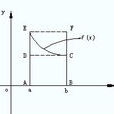
不妨假設是嚴格遞減函式，如上圖所示。

顯然有；

即 ...................................................(1)

根據基本版本的積分中值定理我們知道

至少存在一點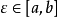，使得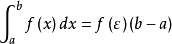..................................(2)

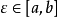
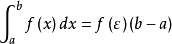
將(2)式代入(1)式可以得到：

由於b>a，上式除以(b-a)可以得到：

再根據函式是嚴格遞減，可以知道：

因此加強版積分中值定理成立。