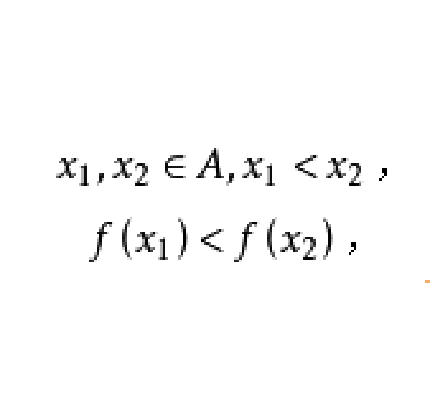嚴格遞增

遞增(increasing)函式是指當函式的任何自變數增加的時候，函式值不減少。嚴格遞增(strongly increasing)是指當函式任何自變數增加的時候函式值也增加。類似地，遞減函式(decreasing)是指當函式的任何自變數增加的時候函式值不增加，嚴格遞減(strongly decreasing)是指當函式任何自變數增加的時候函式值卻減少。

研究數列時，對於一個實數列{u_n}，如果從第2項起，每一項都大於它的前一項，即u_n+1>u_n，則把這樣的實數列稱做嚴格遞增數列；或說這一數列嚴格遞增或嚴格單調增加。

基本介紹

• 中文名：嚴格遞增
• 定義：任意x1.x2,若x1>x2,
• 第2項：每一項都大於它的前一項的數列
• 類別：數學

嚴格遞增函式

定義1

遞增(increasing)函式是指當函式的任何自變數增加的時候，函式值不減少。嚴格遞增(strongly increasing)是指當函式任何自變數增加的時候，函式值也增加。類似地，遞減函式(decreasing)是指當函式的任何自變數增加的時候函式值不增加，嚴格遞減(strongly decreasing)是指當函式任何自變數增加的時候函式值卻減少。

定義2

設 為偏序集， ，如果對任意的 ，都有 ，則稱 為單調遞增的；如果對任意的 ，都有 ，則稱 為嚴格單調遞增的。

類似的，也可以定義單調遞減和嚴格單調遞減的函式。

舉例分析

例1 單調遞增函式的一些例子：

(1)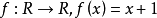 是嚴格單調遞增的；

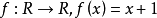
(2)偏序集 ，其中， 為包含關係，≤為一般的小於或等於關係。令 是單調遞增的，但不是嚴格單調遞增的。

嚴格遞增數列

對於一個實數列 ，如果從第2項起，每一項都不小於它的前一項，即有 ，這樣的實數列叫做遞增數列，也叫做上升數列；或說這一數列單調增加．

如果每一項都大於它的前一項，即 ，則把這樣的實數列叫做嚴格遞增數列；或說這一數列嚴格遞增或嚴格單調增加．

對於一個實數列 ，如果從第2項起，每一項都不大於它的前一項，即有 ，這樣的實數列叫做遞減數列，也叫做下降數列，或說這一數列單調減少。

如果每一項都小於它的前一項，即 ，則把這樣的實數列叫做嚴格遞減數列；或說這一數列嚴格遞減或嚴格單調減少．

相關結論

一個嚴格遞增的連續函式，它不處處可微。

下面的例子是由Pringsheim作出的，令

易見， 在 上連續，因為當x≠0時，

所以 在 和 內都是嚴恪遞增的，又當x>0時， ，而當x<0時， ，可見 在 內也是嚴格遞增的，但由於

不存在，因而 在x=0處不可微。

注意:有人或許會猜測，嚴格單調函式的不可微的點都是一些間斷點，上述反例說明了這種猜測是不正確的。