基本介紹
- 中文名:單純同調序列
- 外文名:simplicial homology sequence
- 領域:數學
- 對象:同調群
- 條件:復形偶
- 學科:群論
概念


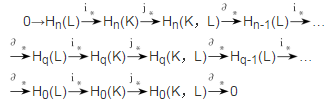


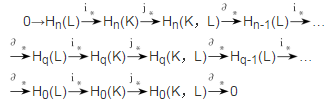
單純同調序列(simplicial homology sequence)是同調群所具有的一種性質。復形偶(K,L)與K和L的各種同調關係表現為它們的同調群組成的一個正合的序列,即單純同調序列,它在單純同調論中有很多套用。...
同時用單純同倫的方法研究一般n維球面同倫群的組合群描述及其與辮群的關係。擬解決的關鍵問題有:譜V(1)對E(3)-同調局部化後的穩定同倫群,經典Adams譜序列中某些元素的收斂與不收斂性。n維球面的同倫群與辮群之間的關係等。
6.2 奇異同調群 習題 6.3 奇異同調群的同倫不變性 習題 6.4 Mayer-Vietoris序列 習題 6.5 同調論的一些套用 習題 6.6 任意係數的同調群與相對同調群 習題 第7章 上同調論 7.1 Hom函子 習題 7.2 單純上同調 習題 7.3 ...
2.1鏈復形及其同調群 2.2鏈映射及其誘導同態 2.3鏈同倫 3奇異同調群 3.1奇異單形 3.2奇異鏈復形與奇異同調群 3.3簡約奇異同調群 3.4奇異同調的同倫不變性 3.5與基本群的關係 3.6u—小奇異鏈 4Mayer—Vietoris同調序列[1]...
《代數的Hochschild同調與同調維數》是依託中國科學院數學與系統科學研究院,由韓陽擔任項目負責人的面上項目。項目摘要 本項目為非交換代數、非交換幾何、同調代數、符號計算的交叉領域。將採用譜序列、超復形塔、同調干擾、非交換Groebner...
序列 ,可生成群同態序列 定義δ:為 則 為切赫鏈復形 。的上同調為切赫上同調 。設 為 的開加細,由限制映射得 ,這與j的選取無關。由歸納極限可得M上的切赫上同調為 性質 若ω∈ ,則 設K為單純復形,M為其底拓撲空間。
然後,我們研究了將多元時間序列轉換為複雜網路,通過考察複雜網路層與層之間的相似性來描述系統組份之間的耦合作用。最後,我們利用代數拓撲中的單純復形對複雜系統開展表征套用,利用拓撲同調性質以及可靠的拓撲指標分析不同網路模型的魯棒性...
《代數拓撲講義》是2007年科學出版社出版的圖書,作者是周建偉。圖書目錄 第1章 基本群 第2章 單純同調群 第3章 奇異同調群 第4章 正契約調序列與切除定理 第5章 奇異上同調與對偶定理 參考文獻 名詞索引 內容簡介 本書內容以基本...
鏈復形(chain complex)是一種抽象的復形。復形常指上復形。上復形亦稱上鏈。一種特殊的模同態序列。類似地可定義和討論與鏈復形有關的鏈映射、鏈同倫以及鏈復形的同調序列等同調理論。從單純同調群和奇異同調群的理論可看出這些...
第六章上同調的Hodge 理論 6.1 物理解釋 6.2 Hodge 星運算元 6.3 Hodge 理論 6.4 離散Hodge 理論 第七章相對同調Mayer-Vietoris 序列 7.1 相對同調和切除定理 7.2 約化同調 7.3 Mayer-Vietoris 序列 7.4 Jordan-Brouwer ...
第三章 相對同調群和Eilenberg.Steenrod公理 23 正合同調序列 24 之字形引理 25 Mayer.Vietoris序列 26 Eilenberg.Steenrod公理 27 單純同調論的公理 28 範疇與函子 第四章 奇異同調論 29 奇異同調群 30 奇異同調論的公...
2.3 上同調論 2.3.1 上同調的實質 2.3.2 上同調群 2.3.3 上同調幾何化定理的證明 2.3.4 同調環的結構 2.4 正合同調序列 2.4.1 相對同調群與切除定理 2.4.2 相關代數理論 2.4.3 同調序列 2.4....
復疊空間及其基本性質,復疊變換與正則復疊空間,單純復形的同調群,同調群的性質,同調群的基本計算,單純映射與單純逼近,重心重分與單純逼近存在定理,連續映射誘導的同調群同態,同調群的同倫不變性,同調序列,球面自映射的映射度,...
數學很大一部分的內在構造可藉鏈復形理解,其性質則以同調與上同調的面貌展現,同調代數能萃取這些鏈復形蘊含的資訊,並表之為拓撲空間、層、群、環、李代數與C*-代數等等“具體”對象的(上)同調不變數。譜序列是計算這些量的有力...
2.3 重心重分和單純逼近 第三章 基本群 3.1 基本群的定義和性質 3.2 計算方法及一些簡單運用 3.3 套用:覆蓋映射和覆蓋空間 第四章 同調群 4.1 單純同調群 4.2 奇異同調群 4.3 正合序列和切除定理 4.4 單純和...
該書論述了代數拓撲中的基礎部分同調論,論證簡潔,內容豐富,是代數拓撲的經典教材。圖書目錄 第一章 阿貝爾群,範疇和同倫 第二章 復形的同調 §1復形 §2 連線同態和正合同調序列 §3 鏈同倫 §4自由復形 第三章奇異同調 §...
數學很大一部分的內在構造可藉鏈復形理解,其性質則以同調與上同調的面貌展現,同調代數能萃取這些鏈復形蘊含的資訊,並表之為拓撲空間、層、群、環、李代數與C*-代數等等“具體”對象的(上)同調不變數。譜序列是計算這些量的有力...
作為另外一個例子,閉流形的最高維的積分上同調群可以探測可定向性:該群同構於整數或者0,分別在流形可定向和不可定向時。這樣,很多拓撲信息可以在給定拓撲空間的同調中找到。在只定義在單純復形的單純同調之上,還可以使用光滑流形的...
