基本介紹
- 中文名:可表示擬陣
- 外文名:representable matroid
- 別稱:可坐標化擬陣
- 所屬學科:數學
- 所屬問題:離散數學(組合序)
- 簡介:一種組合構形
基本介紹
相關介紹

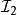


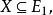


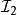


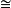
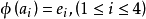
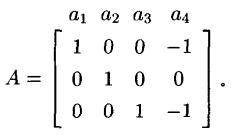
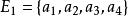
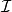
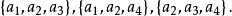
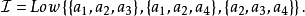
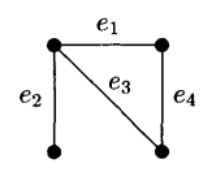
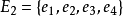
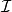
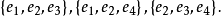
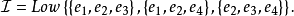
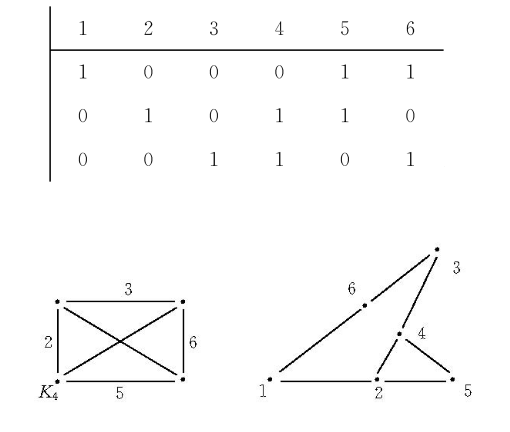
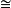
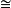




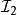


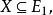


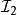


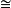
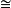
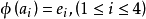
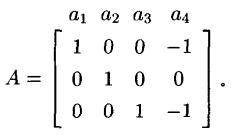
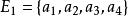
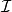
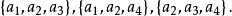
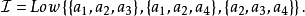

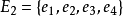
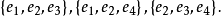
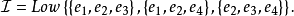
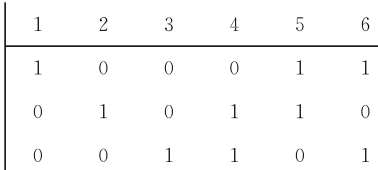
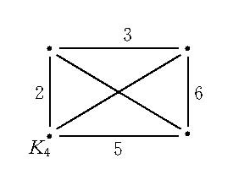
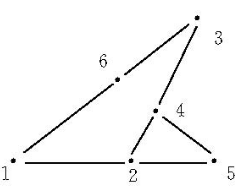
可表示擬陣(representable matroid)亦稱可坐標化擬陣,是一種組合構形,它是與有限域GF(q)上的矩陣擬陣M(A)有一一對應關係的擬陣M(E),稱M(A)為擬陣M(E)的...
Closure operators:設M是有限集E上的一個擬陣,其秩函式有上述定義。E的子集A的閉包cl(A)的定義如下:閉包運算元 擁有如下性質,其中 表示冪集。1. 對於E的所有...
(G)的圈一樣,以G的上圈為圈,對應地得到G上的另一類擬陣,稱為上圈擬陣,上圈擬陣亦稱鍵擬陣,圈擬陣和上圈擬陣互為對偶,且在任何域上均可表示,記上圈擬陣為...
法諾擬陣(Fano matroid)是一種特殊的擬陣,即二元擬陣F7,僅含有7個元素,F7不是單模擬陣,因此,以F7為其子擬陣的擬陣也不是單模擬陣 [1] 。...
本書較為系統地介紹了擬陣論的基本概念和理論,引入和比較了擬陣的不同的公理系統,並較為全面地討論了擬陣的幾何表示、對偶、幼陣、連通度以及擬陣的線性與代數...
擬陣多面體(matroid polytope)是一類多面體,它是擬陣上的最佳化問題所確定的多面體,設U=(J,F)為一個擬陣,其中J為一個有限集,F為獨立集族,對於任何W⊆J,所有...
對偶擬陣(dual matroid)亦稱正交擬陣,是一種組合構形,它是由擬陣M導出的擬陣M*,當擬陣M以基集族B表示時,M=(E,B),則M*=(E,B*),其中B*={E-B:B∈B...
均勻擬陣(uniform matroid)是一種特殊的擬陣,設n≥r≥0是兩個整數,E是一個含有n個元素的集合。如果I={X⊆E:|X|≤r},則稱(E,I)是一個均勻擬陣, 記...
,Em是E上的一個劃分,di是一個正整數。如果I= {X⊆E:|X∩Ei|≤di,1≤i≤m},則稱M(E,I)是一個劃分擬陣(partition matroid)。 [1] ...
匹配擬陣(matching matroid)一類特殊的擬陣.它是建立在圖G=<V,E)上的擬陣.節點集V的子集A為此擬陣的獨立集,若且唯若圖G有匹配覆蓋A.例如,當G為三角形時,...
單模擬陣亦稱正則擬陣,是一類特殊的可表示的擬陣,指在任何域上均可表示的擬陣。擬陣M(E)為單模擬陣,若且唯若M(E)有全單模的表示矩陣。...
擬陣的秩公理(rank axiom of matroid)是刻畫擬陣的一種法則,它是定義在有限集E的子集族上的函式。r所滿足的條件:1.對於E的任意子集X,有r(X)鎮}X}....
多面體擬陣(polymatroid)是一類整多面體,是與擬陣多面體有關的一個概念,可分為有界多面體擬陣和無界多面體擬陣。...
擬陣自環(loop of matroid)一種組合構形.指擬陣中不構成獨立集的單個元素集.當擬陣為圖擬陣M(G)時,擬陣的自環和圖G的自環是一致的.擬陣的自環可等價地描述...
仿射擬陣(affine matroid)是一種組合構形,它是與矩陣擬陣類似的擬陣M(E),不同的是,這裡的E是仿射空間A中的有限點構成的集合,而且在A中沒有真子仿射空間可以...
擬陣超平面公理決定的 ℋ 惟一決定了擬陣的超平面。換言之,E 的真子集 H 為擬陣的超平面,當且僅H∈ℋ ,當 ℋ 決定以後,可由其元素的交集決定出擬陣...
P (M; }l)一習I-}M(},F')·}r(M,一‘F)FE1.這裡I為M之平集組成的格,}M為擬陣M上的默比烏斯函式.當}l= 0時,P(M,0)=}(M),即默比烏斯不...
單形擬陣S分是可表示擬陣,其表示矩陣記為:(n ,k)=(sp,4),為{、二7卜(:!矩陣.其產生方法為,先把((k-1)單形按字典序排列,並以p表示其中之一,再把k...
類似於擬陣中獨立集的相應性質,因此,把以偏截元為其獨立集的擬陣,稱為截元擬陣,對於截元擬陣,其對偶擬陣一般不再是截元擬陣,但是,截元擬陣和匹配擬陣本質上是...
