擬陣多面體

擬陣多面體(matroid polytope)是一類多面體，它是擬陣上的最佳化問題所確定的多面體，設U=(J，F)為一個擬陣，其中J為一個有限集，F為獨立集族，對於任何W⊆J，所有那些在包含意義下的W的極大獨立子集均有相同的基數，即所含元素的數目相同，並且稱這個數為W的秩，記為r(W)，擬陣的秩函式r是次模的，即對任何X，Y⊆J，均有r(X∪Y)+r(X∩Y)≤r(X)+r(Y)，多面體M(r)={x∈E⁺_n|∑_i∈wx_i≤r(w)，對任何w⊆N}，其中N={1，2，…，n}，n=|J|，就稱為擬陣多面體。

基本介紹

• 中文名：擬陣多面體
• 外文名：matroid polytope
• 所屬學科：數學
• 所屬問題：離散數學（組合序）
• 簡介：擬陣上的最佳化問題所確定的多面體

基本介紹

擬陣多面體是一種組合構形，它是由擬陣M=(E，I)的所有獨立集的關聯向量生成的多面體P。

記E={e₁，e₂，…，e_n}，獨立集I的關聯向量v(I)=(v₁，v₂，…，v_n)，當I包含元素e_i時，v_i=1，否則v_i=0，擬陣多面體的優越性在於，它可以藉助擬陣的秩函式r而表示為約束不等式的形式I(E，r)：對於E的任意子集F，有

且對於E的任意元素e，有x_e≥0，擬陣多面體P的頂點均為整值點，這樣建立在擬陣上的最佳化問題就可以歸結為不考慮其解是否取整數值的一般線性規劃問題，從而為擬陣上的最佳化問題開闢了一個新的領域，例如，下圖G上的圖擬陣M(G)，其多面體由下述不等式決定：

x_e1≤1，x_e2≤1，x_e3≤1，x_e4≤1，

x_e1+x_e4≤2，

x_e2+x_e4≤2，

x_e3+x_e4≤2，

x_e1+x_e2+x_e3≤2，

x_e1+x_e2+x_e4≤3，

x_e1+x_e3+x_e4≤3，

x_e2+x_e3+x_e4≤3，

x_e1+x_e2+x_e3+x_e4≤3，

x_e1≥0， x_e2≥0， x_e3≥0， x_e4≥0.

圖1

在以約束不等式表示的擬陣多面體裡，若以G的滿足下述條件的一般整值次模函式f取代擬陣的秩函式：

1.f(∅)=0；

2.對於E的任意子集A，B，若A⊆B則：

f(A)≤f(B)；

3.對於E的任意子集A和B，有

則不等式組I(E，f)決定的多面體，其頂點仍對應於某個擬陣的獨立集，由I(E，f)決定的擬陣稱為多面體擬陣。

相關介紹

多面體擬陣是一類整多面體，設為n維歐氏空間的那個非負象限，在上定義一個偏序：對於x，y∈，x≤y表示x_i≤y_i，i=1，2，…，n，設D⊆，若x₀∈D具有這樣的性質：不存在x∈D，x≠x₀，使得x≤x₀，則稱x₀為偏序D上的一個極小元，若不存在x∈D，x≠x₀，使得x≥x₀，則x₀為D上的一個極大元，在上的一個有界多面體擬陣就是這樣的一個多面體M，它具有性質：

1.若0≤y≤x，x∈M，則y∈M；

2.對任何a∈，集合M_a={x∈M|x≤a}的所有極大元的分量和均相同，並且，這個和稱為a的秩；

在上所定義的秩確定一個多面體擬陣的秩函式，在N={1，2，…，n}的所有子集形成的簇2^N上定義的函式ρ，若對任何U，W∈2^N均有

ρ(U)+ρ(W)≥ρ(U∪W)+ρ(U∩W)，

則稱ρ為次模的，若上面的不等式是反向的，則稱ρ為上模的，一個多面體M⊆是有界多面體擬陣，若且唯若在2^N上存在一個非降的次模函式ρ(W)，ρ(∅)=0，使得

M={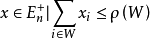，對任何W⊆N}.

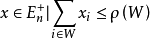
在上的一個無界多面體擬陣就是這樣的一個多面形Q，使它具有性質：若y≥x，和x∈Q，則y∈Q;對任何a∈，在Q_a={x∈Q|x≥a}中的每個極小元的分量和都相同.一個多面形Q⊆是一個無界多面體擬陣，若且唯若存在2^N上的一個上模函式ρ(W)，ρ()=0，使得

Q={，對任何W⊆N}.