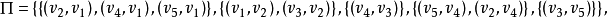設e是一個非空有限集合，E1，E2，…，Em是E上的一個劃分，di是一個正整數。如果I= {X⊆E：|X∩Ei|≤di，1≤i≤m}，則稱M(E，I)是一個劃分擬陣(partition matroid)。
基本介紹
- 中文名：劃分擬陣
- 外文名：partition matroid
- 所屬學科：數學
- 所屬問題：組合學（組合序）
- 簡介：一種組合構形
基本介紹,舉例說明,
基本介紹
若劃分π把E分割為劃分塊B1，B2，…，Bm，並相應地設定非負整數d1，d2，…，dm，則E的子集I為劃分擬陣的獨立集，若且唯若對於i=1，2，…，m，均有|I∩Bi|≤di。
例如對於有向圖G=(V，A)，A的子集I為這樣一類集合：I中沒有兩條邊同指向一個節點，以這樣的I為獨立集可得一划分擬陣，相應地，J為A的這樣一類集合：J中沒有兩條邊始於同一節點，以這樣的J為獨立集可得另一划分擬陣。
舉例說明
例1 設E是一個有限集，∏是E的一個劃分，即∏={E1，E2，…Ep}為E的不相交子集的集合，並且覆蓋E。E的一個子集I稱為是獨立的(I∈F)，若且唯若I中任何兩個元素不在∏的同一個集合里，即對一切j=1，2，…，p，|I∩Ej|≤1。則M∏=(E，F)為一個擬陣，並稱其為劃分擬陣。
要證明M∏是一個擬陣，只要證明它有明確定義的秩函式即可。令J(A)={j≤p：Ej∩A≠∅)，讀者容易驗證，r(A)=|J(A)|是滿足要求的秩函式。事實上，對於E的任一個子集A，我們可構造A的極大獨立子集如下：對於使Ej∩A≠∅的每一個Ej，我們在Ej中選取A的一個元素，那么所選取的元素集合，就是A的一個極大獨立集。例如，若E={e1，…，e8}，∏=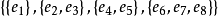
，那么
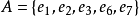在M∏中的秩為3，A的極大獨立集為
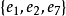，A的支撐
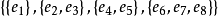
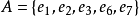
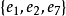
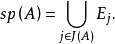
對每一個j，集合Ej中任意兩個元素就構成M∏的一個圈。因此，{e2，e3}和{e6，e8}都是M∏的圈。
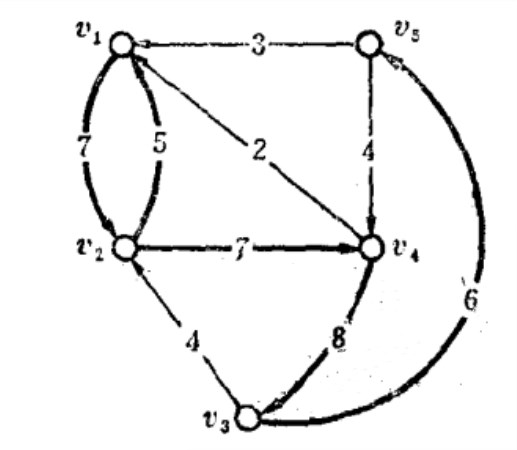
例2 給定一個有向圖(V，A)，對每一孤a∈A有一個權w(a)≥0。希望找出A的一個最大權的子集B，使得B中任何兩條弧都沒有公共的終點。這是關於子集系統(A，B)的一個組合最佳化問題，其中A的一個子集B∈B，若且唯若B中任何兩條弧都沒有公共的終點。這一問題看起來很象無向圖的匹配同題，但是它比匹配問題容易得多。例如在圖1中，選取進入v1的弧時，只要挑選一個最大權的即可。因為選取進入一個點的任何一條弧，對於選取進入其它點的弧沒有影響，故greedy算法能得到該問題的最優解。
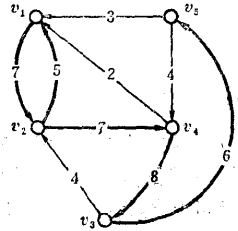
例2中的子集系統，是劃分擬陣的另一個例子。在圖1上的有向圖D中，設B是D中弧的一個集合，若B中任何兩條弧都不指向同一個節點，則稱B為獨立集。這就等價於把D的弧進行劃分，使得指向同一節點vj的弧之集合定義為Ej。在這個例子中，下述定義的∏為D的弧集的一個劃分：
