匹配理論

匹配理論（Matching theory）是個體經濟學的領域之一，主要研究匹配相關的性質，如匹配的穩定性，匹配機制以及匹配機制中參與人的策略與對應的均衡結構等內容。

基本介紹

• 中文名：匹配理論
• 外文名：Matching theory
• 所屬學科：個體經濟學

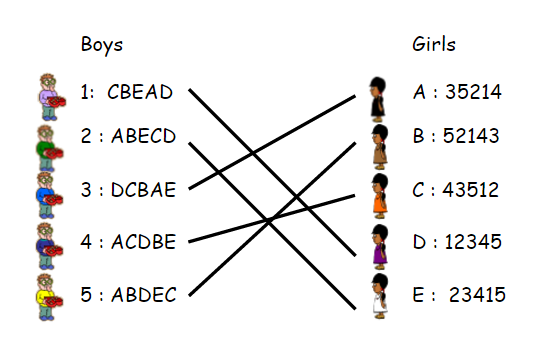
簡介

匹配是日常生活中常見的現象，如市場上買方和賣方相互匹配，婚姻中男性和女性相互匹配，學校中學生相互匹配組成寢室等。匹配理論的創始人之一是西北大學的Dale T. Mortensen。一本關於勞動力市場匹配方法的教科書是ChristopherA. Pissarides的《均衡失業理論》。Mortensen和Pissarides與Peter A. Diamond一起被授予2010年諾貝爾經濟學獎，以表彰他們“對搜尋和匹配理論的基本貢獻”。匹配理論最早的理論研究可以追溯到1962年David Gale與LloydS. Shapley的論文《大學招生和婚姻的穩定性》，在此之後Alvin Roth明確給出了雙邊匹配的定義，做出了一系列重要的研究，並於2012年與Shapley因“穩定分配理論與市場設計的實踐”共同獲得諾貝爾經濟學獎。匹配理論可以用於指導設計資源匹配機制，以實現資源的有效分配和利用，並已在器官移植，無線通信等多個領域得到了實際套用。

匹配理論的重要課題之一是雙邊匹配問題，其中雙邊指的是匹配關係是建立在兩個不交的集合之間的，例如婚姻關係中男性集合與女性集合是不交的；而匹配是指這種關係是雙向的，例如如果我為一家公司工作，那么這家公司就雇用了我。由此可知：市場中如果有人既是買方也是賣方，那么賣出與買入的關係不構成雙邊匹配；男性與女性之間的婚姻關係構成一對一的雙邊匹配；勞動力市場上僱主與雇員構成一對多的雙邊匹配；學生互相匹配組成寢室不是雙邊匹配。下面簡要介紹一對一的雙邊匹配的理論。

一對一匹配

婚姻模型

考慮男性與女性之間婚姻關係構成的雙邊匹配，此時匹配關係是一對一的，也即一位男性與一位女性相匹配。設M代表男性集合，代表集合中的一位男性；W代表女性集合，代表集合中的一位女性，那么一個匹配如下所示：

，

:

匹配就代表了與配對，與配對，與配對。

下面考慮個體的偏好，也即個體更傾向於和誰匹配，在婚姻模型中這意味著男性更願意和哪位女性結婚，以及女性更願意和哪位男性結婚。例如的偏好可以記為：

意味著會優先選擇與結婚，其次是，再次是。不妨設6人偏好如下：

並假設他們形成了匹配，此時與配對，與配對，但是相比現在的匹配對象更希望與匹配，且相比現在的匹配對象也更希望與匹配。那么此時與有充分的動機打破當前的匹配並互相匹配在一起，我們稱此時匹配不是穩定的，是它的破壞配對。此處可以看出破壞配對的含義：破壞配對在匹配中是未相互配對的，且相對於他們當前的伴侶都更喜歡對方。

:

在了解婚姻匹配的穩定性後，一個自然的問題是：給定男性和女性的集合，以及每名男性或者女性的偏好後，穩定的婚姻匹配是否一定存在？如果存在如何求出一個穩定匹配？Gale與Shapley給出的延遲接受算法回答了上面的問題。

延遲接受算法

延遲接受算法說明了穩定婚姻匹配的存在性，並給出了一個穩定的婚姻匹配，它的主要流程如下：

1. 每位男性向他最偏好的女性求婚，此時每位女性可能會被求婚不止一次，但她只接受所有求婚者中她最偏好的那一位。但是這種接受是暫時的，也即沒有被拒絕的男性和相匹配的女性只是“訂婚”了，之後如果女性被她更偏好的男性求婚，那么她就會轉而與更偏好的男性“訂婚”。這正是“延遲接受”的含義。
2. 所有被拒絕的男性向自己下一級偏好的女性求婚，每位女性只接受所有求婚者中她最偏好的那一位。重複此步驟多次，直到沒有男性被拒絕，算法停止。

首先此算法一定會停止，這是因為男性和女性集合都是有限的，且每位男性對某位女性最多只求婚一次。其次此算法給出的匹配一定是穩定的，這是因為：假設算法給出的匹配中與不是相互匹配的，且相比自己當前的伴侶更喜歡對方，那么一定在向自己當前伴侶求婚之前一定已經向求過婚，但是因為有比更好的選擇而被拒絕了。故不存在這樣的破環配對，匹配是穩定的。

不妨以上一節中的偏好為例展示延遲接受算法的流程：

第1次求婚後，由於和都向求婚，此時只接受她更喜歡的，而拒絕了，匹配情況如下：

第2次求婚只有被拒絕的向他下一級偏好的女性求婚，而直接接受，此時沒有男性被拒絕，算法停止，得到的穩定匹配記為：

更多性質

• 延遲接受算法的性質

在上述例子中，男性和女性集合大小是相等的，且個人的偏好是嚴格，且沒有考慮到個人與其與某人匹配寧願單身的情形。但實際上這些因素均不影響穩定婚姻匹配的存在性，且只需對算法稍加改動（如男性只向可接受的女性求婚，若已經被所有可接受的女性拒絕就不再求婚，保持單身）就可以包含這些情況。

我們還可以發現由於男性與女性在婚姻匹配問題中的地位是對等的，將上述算法中男性主動求婚，女性延遲接受改為女性主動求婚，男性延遲接受可以得到另一生成穩定匹配的算法，事實上此算法生成的穩定匹配正是與不同的。對比與可以發現中每一位男性都相比中獲得了同樣好或更好的匹配：相比更喜歡，匹配結果相同，相比更喜歡。且中每一位女性都相比中獲得了同樣好或更好的匹配。這並不是一個巧合，我們有下面的定理：

定理：若所有的男性和女性的偏好都是嚴格的，那么總會存在一個男性最優穩定匹配和一個女性最優穩定匹配。且由男性求婚的延遲接受算法得到的穩定匹配正是男性最優穩定匹配，由女性求婚的延遲接受算法得到的穩定匹配正是女性最優穩定匹配。

• 不可能性定理

延遲接受算法實際上給出了一種穩定匹配機制，這意味著所有男性和女性只需提交自己的偏好，機制就可以給出一個穩定婚姻匹配方案。然而此時個體真的會提交自己真實的偏好嗎，換言之，個體提交一個不真實的偏好是否有可能獲得一個更好的匹配結果，從而有動機謊報偏好？這樣的情況確實可能出現，若使用博弈論的模型，將婚姻匹配視為一次靜態博弈，最終獲得怎樣的匹配對象可以視為個體的收益，而個體的可選的策略是提交不同偏好，那么提交自己真實的偏好並不總是占優策略。那么有可能設計一個穩定匹配機制使得每位參與人提交自身的真實偏好總是占優策略嗎？Roth在1982年通過下面的定理，給出了否定的答案：

定理：不存在穩定匹配機制使得對每個參與人來說提交真實偏好都是占優策略。

套用案例

器官移植

器官移植是某些疾病的重要治療方法，但相比需要移植器官的患者數量，可供移植的器官數量非常有限。即使病人家屬有捐獻器官的意願，但由於受體和供體之間必須在血型等多方面相互匹配，家屬並不一定能夠提供有效的捐獻。Roth等人研究了交換捐獻器官的可能性，即有意願捐獻器官的家屬由於免疫排斥等原因無法將器官捐獻給病人，但是可以在交換捐獻機制下將器官捐獻給相匹配的其他病人，作為回報，病人將獲得來自其他捐獻者的相匹配的可移植器官。Roth等人發現其中捐獻者-病人對之間的匹配問題類似機制設計中分配不可分物品的問題，並說明了交換捐獻機制下病人可能獲得更多數量以及更高質量的可移植器官。這一機制已經在美國的一些地方實際開始運行。