霍爾定理，此定理用在組合數學中，又稱霍爾婚配定理，由飛利浦· 霍爾於1935年證明。
基本介紹
- 中文名：霍爾定理
- 外文名：Hall theorem
- 別稱：霍爾婚配定理
- 證明者：飛利浦·霍爾
- 時間：1935年
霍爾定理簡述,霍爾定理詳解,
霍爾定理簡述
霍爾定理： 此定理使用於組合問題中；二部圖G中的兩部分頂點組成的集合分別為X, Y,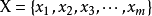 
， 
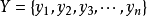，G中有一組無公共點的邊，一端恰好為組成X的點的充分必要條件是： X中的任意k個點至少與Y中的k個點相鄰。（1≤k≤m) 本論還有一個重要推論： 二部圖G中的兩部分頂點組成的集合分別為X,Y, 若∣X∣=∣Y∣,且G中有一組無公共端點的邊，一端恰好組成X中的點，一端恰好組成Y中的點， 則稱二部圖G中存在完美匹配。若圖G的每個點度數為t，則稱二部圖G為t---正則的二部圖存在完美匹配。 本定理是二分圖匹配問題中匈牙利算法的基礎。
霍爾定理詳解
設給定任意集合S和S的子集的任意有限系(1):
子集系(1)的相異代表元的一個完全集[complete set of distinet representatives，簡記為C.D.R.——這是霍爾的原始用語，後來的文獻一般稱為相異代表系(system of distinet representatives)，簡記為SDR]是指S的m個相異元素的一個集合: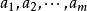
，使得對於每個
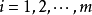，有英國數學家霍爾(P.Hall，1904——1982)在1935年發表的“論子集的代表元中指出：“為使(1)存在一個C.D.R.，則下面的條件是充分的，即對每個
，任意選取(1)的k個集合，其中都將包含至少k個S的元素.”由於此前霍爾已經指出該條件的必要性是顯然的，因此他給出的實際上是一個充要條件。至於以圖論術語表述的霍爾定理，則可以在貝爾熱的《圖的理論及其套用》(1955)中找到原型：“(設G是一個具有二分部(X，Y)的二部圖，R(A)表示
時Y中與A的至少一個點相鄰接的點的集合，)X能被匹配到y若且唯若對於所有的集合
有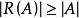
。”
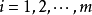
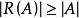
霍爾定理有時也被人們稱為“婚配定理”，因為它對於美國數學家哈爾莫斯(P.R.Halmos，1916一2006)和法烏甘(H.E.vaughan)在“婚配問題”(1950)一文中所表述的如下問題：“假設一批小伙兒中的每一位都與一定數目的姑娘相識，問在什麼條件下每位小伙兒都能與他認識的一位姑娘結婚？”提供了解答，即必須要使任意一組無個小伙兒認識至少k個姑娘.因此霍爾定理的條件有時也被稱為“婚配條件”.然而“婚配問題”的提法最早卻出自德國數學家外爾(H.Weyl，1885一1955)的一篇文章。
“婚配定理”這一名稱也常被賦予屬於柯尼希四的下述定理：“每個正則二部圖都具有一個一度因子；每個k度正則二部圖都可分離出k個一度因子。”它們可作為霍爾定理的推論。這時相應的婚配問題也常以“跳舞問題”的面目出現：“設有n個男孩和n個女孩的一次聚會，每個男孩恰好認識其中的k個女孩，每個女孩也恰好認識其中的k個男孩.間有沒有可能使他們跳舞時都與彼此認識的人結成舞伴?’’上述推論對此給出了肯定的回答。
