基本介紹
- 中文名:列維-奇維塔聯絡
- 外文名:Levi-Civita connection
- 領域:數學
簡介
黎曼幾何
偽黎曼流形

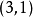

形式化定義

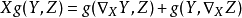



沿曲線的導數

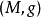



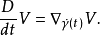

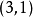


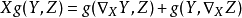




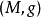



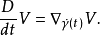
列維-奇維塔聯絡(Levi-Civita connection),在黎曼幾何中, 是切叢上的無撓率聯絡,它保持黎曼度量(或偽黎曼度量)不變。因義大利數學家圖利奧·列維-奇維塔而得名。...
聯絡是接洽和聯繫的同義詞,是互相之間取得聯通關係的意思,一般指彼此交接;接上...稱一個無撓聯絡為列維-奇維塔聯絡,如果(4)X(Y,Z)=(D(X)Y,Z)+(Y,D(...
表示 有仿射聯絡的流形的曲率 包括 無撓率或有撓率的目錄 1 簡介 2 對稱性和恆等式 黎曼曲率張量簡介 編輯 曲率張量通過列維-奇維塔聯絡(更一般的,一個仿射聯...
在黎曼和偽黎曼流形理論中,共變導數通常指列維-奇維塔聯絡。 這裡,我們給出一個向量相對於向量場的共變導數(也稱為張量導數)的傳統的帶指標記號的簡介;張量的共...
稱一個無撓聯絡為列維-奇維塔聯絡,如果(4)X(Y,Z)=(D(X)Y,Z)+(Y,D(X)Z),(,)為黎曼度量。 [3] 和樂群群 編輯 群是一種只有一個運算的、比較...
給定一個參數化測地線系統,我們一定指定一族仿射聯絡具有這些測地線,但是具有不同的撓率。具有惟一“吸收撓率”的聯絡,將列維-奇維塔聯絡推廣到其他,也許沒有度量的...
利用與列維-奇維塔聯絡相伴的共變導數,拉普拉斯–貝爾特拉米運算元可推廣到偽黎曼流形上任意張量。這個推廣的運算元可以作用在反對稱張量上。但所得的運算元與拉普拉斯–德...
這使得我們能夠在偽黎曼流形上能夠使用列維-奇維塔聯絡和相關的曲率張量。另一方面,黎曼幾何的很多定理在推廣到偽黎曼的情況下不成立。例如,並不是每個光滑流形都...
其中∇是向量叢TM⊗φ上由M和N的列維-奇維塔聯絡導出的聯絡。式中τ(φ)是向量叢φ(TN)的截面,稱為φ的張力場。用上文的物理比喻來說,τ(φ)是“橡膠...
這使得我們能夠在偽黎曼流形上能夠使用列維-奇維塔聯絡和相關的曲率張量。另一方面,黎曼幾何的很多定理在推廣到偽黎曼的情況下不成立。例如,並不是每個光滑流形都...
如果是黎曼流形(就是有度量的流形),則可以唯一定義一種聯絡,稱為列維-奇維塔聯絡,從而有了一種協變微分定義。詞條標籤: 物理學 , 學科 ...
與向量叢的每個基相伴的聯絡形式是微分1-形式矩陣。聯絡形式沒有張量性因為在基變化下,聯絡形式的變換涉及到轉移函式的外微分,與列維-奇維塔聯絡的克里斯托費爾符號...
在廣義相對論中,作用量一般都被認為是度規(以及物質場)的一個泛函,而其聯絡是列維-奇維塔聯絡。能夠導出真空中的愛因斯坦方程的作用量 由下面的拉格朗日量的積分...
黎曼流形的曲率的標準方式,更普遍的,它可以表示有仿射聯絡的流形的曲率 ,包括...曲率張量通過列維-奇維塔聯絡(更一般的,一個仿射聯絡) (或者叫協變導數)由下...
