基本介紹
- 中文名:閔可夫斯基空間
- 外文名:Minkowski space
- 別稱:閔可夫斯基時空
- 領域:數學
- 提出者:閔可夫斯基
- 提出時間:1909年
簡介
定義

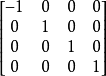
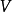


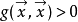
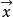

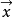
推導
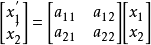
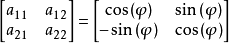
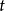


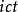


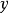
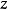
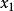
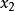
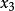


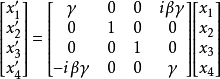
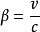


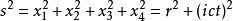

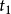
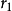
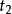

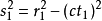


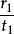
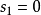

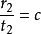





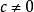


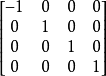
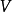


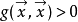
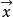

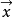
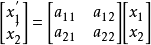
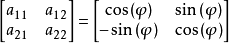
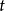


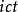


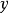
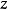
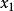
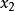
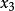


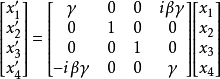
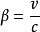


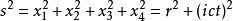

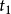
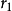
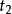

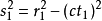


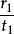
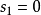

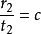





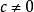
閔可夫斯基空間是狹義相對論中由一個時間維和三個空間維組成的時空,它最早由俄裔德國數學家閔可夫斯基(H.Minkowski,1864-1909)表述。他的平坦空間(即假設沒有重力...
四維空間不同於三維空間,四維空間指的是標準歐幾里得空間,可以拓展到n維;四維時空指的是閔可夫斯基空間概念的一種誤解。人類作為三維物體可以理解四維時空(三個空間...
時空圖,又稱閔可夫斯基圖,用以表示閔可夫斯基時空的事件的坐標。它是一種理解狹義相對論現象的工具。...
引力的作用就在於使空時變成彎曲的,而不再是經典力學中的無限延伸的歐幾里得幾何的絕對空間和無限延伸的閔可夫斯基空間 [1] 。廣義相對論揭示存在空間-時間客體,...
閔可夫斯基(Hermann Minkowski,1864-1909)出生於俄國的 Alexotas (現在變成立陶宛的 Kaunas)。父親是一個成功的猶太商人,但是當時的俄國政府迫害猶太人,所以當閔...
閔氏空間指狹義相對論中由一個時間維和三個空間維組成的時空,為俄裔德國數學家閔可夫斯基(H.Minkowski,1864-1909)最先表述。他的平坦空間(即假設沒有重力,曲率...
閔可夫斯基的時空幾何是不符合歐幾里得體系的,所以也就與當前的研究沒有關係。從數學方面講,普通三維空間集合的四維等價物是歐幾里得四維空間,一個四維歐幾里得賦范...
而相對論的誕生以及相應的數學描述:閔可夫斯基時空將時間和空間整體地作為四維的連續統一體進行看待。三次元是ACGN次文化中對於現實世界或以現實世界為基礎的人物、...
《閔氏幾何與狹義相對論》中用閔可夫斯基時空幾何圖為工具,論述了狹義相對論的原理、運動學效應和時空觀。作為一個獨立的研究成果,給出了直接用“光格面積”度量...
閔可夫斯基,外國人名字中的姓氏,著名的有德國數學家、德國醫學家和美籍德裔天文學家。 閔可夫斯基本人則因數學才能出眾,早有神童之名,後來更是優秀的數學家。...
而相對論以及相應的數學描述:閔可夫斯基時空將時間和空間整體地作為四維的連續統一體進行看待。弦理論問世以後,用三維空間來描述現實中的宇宙已經不再足夠,而需要用...
彭羅斯圖也叫做共形圖或直接被稱為時空圖。彭羅斯圖性質 編輯 對於局部的漸近平直時空(所謂漸近平直,是指當坐標趨於無限遠時時空曲率趨於零,即閔可夫斯基時空),...
在粒子物理學中常用的、平坦的閔可夫斯基時空中,拓撲場論並不十分有趣。這是由於閔可夫斯基空間可以被收縮成一點,所以其中的TQFT只計算出平凡的拓撲不變數。因此,...
但是,這一點未能考慮到宇宙並不是平滑,靜止,而且符合閔可夫斯基時空的狹義相對論的。事實上宇宙時空由於膨脹而變得彎曲,正如哈勃定律揭示的那樣,光的速度乘以宇宙...
全書共十章,前五章介紹了芬斯勒流形、閔可夫斯基空間(即芬斯勒流形的切空間)上的幾何量、陳聯絡,以及共變微分和第二類幾何量、黎曼幾何不變數和弧長的變分等...
四維矢量,是在狹義相對論里,四維矢量 (four-vector) 是實值四維矢量空間裡的矢量。這四維矢量空間稱為閔可夫斯基時空。四維矢量的分量分別為時間與三維位置。在閔...
擴展物理學中,彎曲時空中的麥克斯韋方程組制約著彎曲時空(其間的度規可能不是閔可夫斯基性的)中的電磁場的動力學。它們可以被認為是真空中的麥克斯韋方程組在廣義...
