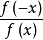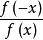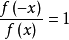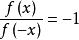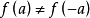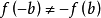定義
⑴如果對於函式
定義域內的任意一個x,都有
或
那么函式
就叫做
偶函式。關於y
軸對稱,
。
⑶
如果對於
函式定義域內的任意一個x,都有
和
,(x∈R,且R關於原點對稱.)那么函式
既是奇函式又是偶函式,稱為既奇又偶函式。
⑷如果對於
函式定義域內的存在一個a,使得
,存在一個b,使得
,那么函式
既不是奇函式又不是偶函式,稱為
非奇非偶函式。
說明:①奇、偶性是函式的整體性質,對整個定義域而言。
②奇、偶函式的定義域一定關於原點對稱,如果一個函式的定義域不關於原點對稱,則這個函式一定不具有
奇偶性。
(分析:判斷函式的奇偶性,首先是檢驗其定義域是否關於原點對稱,然後再嚴格按照奇、偶性的定義經過化簡、整理、再與
比較得出結論)
③判斷或證明函式是否具有奇偶性的根據是定義。
④如果一個奇函式
在x=0處有意義,則這個函式在x=0處的函式值一定為0。並且關於
原點對稱。
⑤如果函式定義域不是關於原點對稱或不符合奇函式、偶函式的條件則叫做非奇非偶函式。例如
⑥如果函式既符合奇函式又符合偶函式,則叫做既奇又偶函式。例如
註:任意常函式(定義域關於原點對稱)均為偶函式,只有
是既奇又偶函式
特徵
概述
偶函式:若對於定義域內的任意一個x,都有f(-x)=f(x),那么f(x)稱為偶函式。
奇函式:若對於定義域內的任意一個x,都有f(-x)=-f(x),那么f(x)稱為奇函式。
定理奇函式的圖像關於原點成中心對稱圖表,偶函式的圖象關於y軸成軸對稱圖形。
f(x)為奇函式《==》f(x)的圖像關於原點對稱
點(x,y)→(-x,-y)
奇函式在某一區間上單調遞增,則在它的對稱區間上也是單調遞增。
偶函式在某一區間上單調遞增,則在它的對稱區間上單調遞減。
奇函式
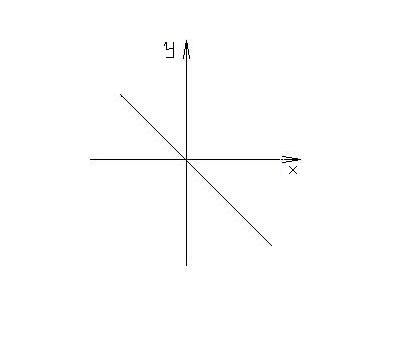 奇函式
奇函式f(x)為奇函式<=>f(x)的圖象關於原點對稱,如圖:
奇函式在某一區間上單調遞增,則在它的對稱區間上也是單調遞增。
點(x,y)→(-x,-y)
奇函式圖像關於原點對稱
偶函式
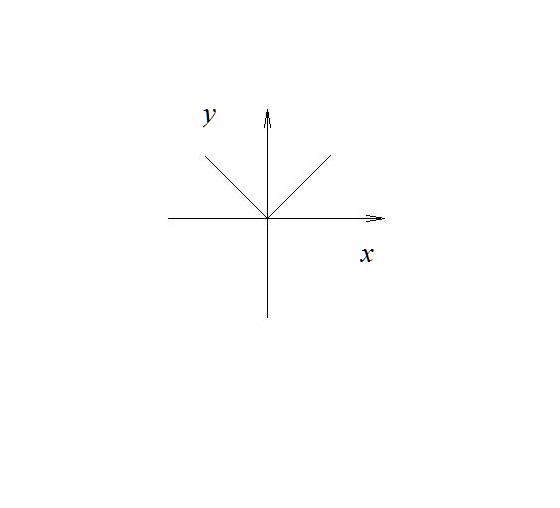 偶函式
偶函式f(x)為偶函式<=>f(x)的圖象關於Y軸對稱,如圖
點(x,y)→(-x,y)
偶函式在某一區間上單調遞減,則在它的對稱區間上單調遞增。
偶函式關於Y軸對稱
證明方法
1、利用奇偶函式的定義來判斷(這是最基本,最常用的方法)定義:如果對於函式y=f(x)的定義域A內的任意一個值x,都有f(-x)=-f(x)則這個函式叫做奇函式f(-x)=f(x),則這個函式叫做偶函式
2、用求和(差)法判斷:
若f(x)-f(-x)=2f(x),則f(x)為奇函式。
若f(x)+f(-x)=2f(x),則f(x)為偶函式。
3、用求商法判斷
性質
1、大部分偶函式沒有反函式(因為大部分偶函式在整個定義域內非單調函式)。

2、偶函式在定義域內關於y軸對稱的兩個區間上單調性相反,奇函式在定義域內關於原點對稱的兩個區間上單調性相同。
3、奇±奇=奇(可能為既奇又偶函式) 偶±偶=偶(可能為既奇又偶函式) 奇X奇=偶 偶X偶=偶 奇X偶=奇(兩函式定義域要關於原點對稱).
4、對於F(x)=f[g(x)]:
若g(x)是偶函式且f(x)是偶函式,則F[x]是偶函式。
若g(x) 是偶函式且f(x)是奇函式,則F[x]是偶函式。
若g(x)是奇函式且f(x)是奇函式,則F[x]是奇函式。
若g(x)是奇函式且f(x)是偶函式,則F[x]是偶函式。
5、奇函式與偶函式的定義域必須關於原點對稱。
要點詮釋
[1]奇偶性是整體性質;
[2]x在定義域中,那么-x在定義域中嗎?----具有奇偶性的函式,其定義域必定是關於原點對稱的;
[3]f(-x)=f(x)的等價形式為:f(x)-f(-x)=0,
(f(x)≠0)
f(-x)=-f(x)的等價形式為:f(x)+f(-x)=0;
(f(x)≠0)
[4]由定義不難得出若一個函式是奇函式且在原點有定義,則必有f(0)=0;
[5]既是奇函式,又是偶函式的函式有無數個,只要f(x)=0,且定義域關於原點對稱即可
常用結論
(2)若f(x-a)為奇函式,則f(x)的圖像關於點(a,0)對稱
若f(x-a)為偶函式,則f(x)的圖像關於直線x=a對稱
(3)在f(x),g(x)的公共定義域上:奇函式±奇函式=奇函式
偶函式±偶函式=偶函式
奇函式×奇函式=偶函式
偶函式×偶函式=偶函式
奇函式×偶函式=奇函式
上述奇偶函式乘法規律可總結為:同偶異奇


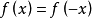
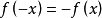

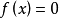


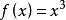
 奇函式
奇函式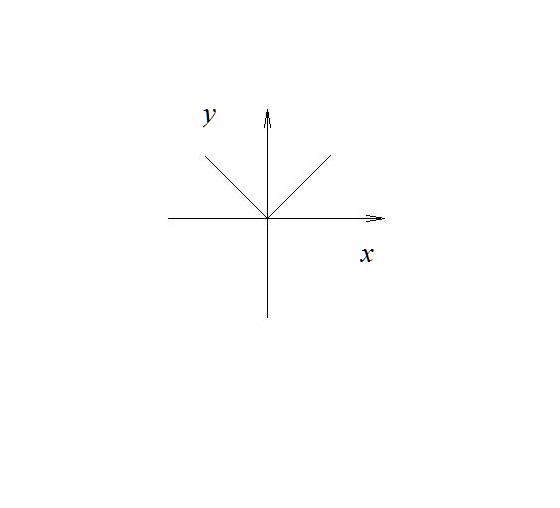 偶函式
偶函式