對勾函式

對勾函式是一種類似於反比例函式的一般雙曲函式，是形如f(x)=ax+b/x（a×b>0）的函式。由圖像得名，又被稱為“雙勾函式”、“勾函式”、"對號函式"、“雙飛燕函式”等。因函式圖像和耐克商標相似，也被形象稱為“耐克函式”或“耐克曲線”。

基本介紹

• 中文名：對勾函式
• 別稱：勾函式、魚鉤函式、耐克函式、雙勾函式、對號函式、雙飛燕函式等
• 表達式：f(x)=ax+b/x (a>0,b＞0)
• 套用學科：數學
• 適用領域範圍：代數學 函式
• 適用領域範圍：解析幾何

函式定義

對勾函式是指形如（a>0，b>0)的函式.

對勾函式

性質

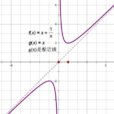
圖像

對勾函式的圖像是分別以y軸和y=ax為漸近線的兩支曲線，且圖像上任意一點到兩條漸近線的距離之積恰為漸近線夾角(0-180°)的正弦值與|b|的乘積.

在第一象限內，其轉折點為.

最值

當定義域為時，（a>0, b>0)在處取最小值，最小值為.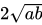

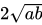
當定義域為時，該函式無最值。

奇偶、單調性

奇偶性

對勾函式是奇函式.

單調性

令k=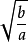，那么：

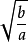
增區間：{x|x≤-k}和{x|x≥k}；減區間：{x|-k≤x<0}和{x|0<x≤k}

變化趨勢：在y軸左邊先增後減，在y軸右邊先減後增.

推導過程

1.導數法

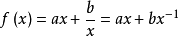
求導得

令f'(x)=0，計算得

即對勾函式的轉折點橫坐標分別為,.

2.均值不等式法

當時，

由均值不等式,(a>0,b>0)

將 中 看做a， 看做b代入上式，得

若且唯若,即時等號成立.

故當x>0時，對勾函式的轉折點橫坐標為.