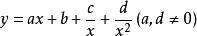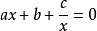定義
函式解析式
SP函式共有三種形式的解析式。
(1)一般式
 a, b, c 對SP函式的影響
a, b, c 對SP函式的影響 a:控制開口大小;
b:控制函式的上下移動;
c:控制函式與坐標軸的距離。
實質:由一般式可以看出,SP函式可看做一次函式和反比例函式的結合。
(2)方程式
通過此形式,可以看出SP函式與
一元二次方程有一定的必然聯繫。
(3)關係式
通過此形式,可以看出SP函式與
二次函式有一定的必然聯繫。
性質
(1)a,c 同號,有端點
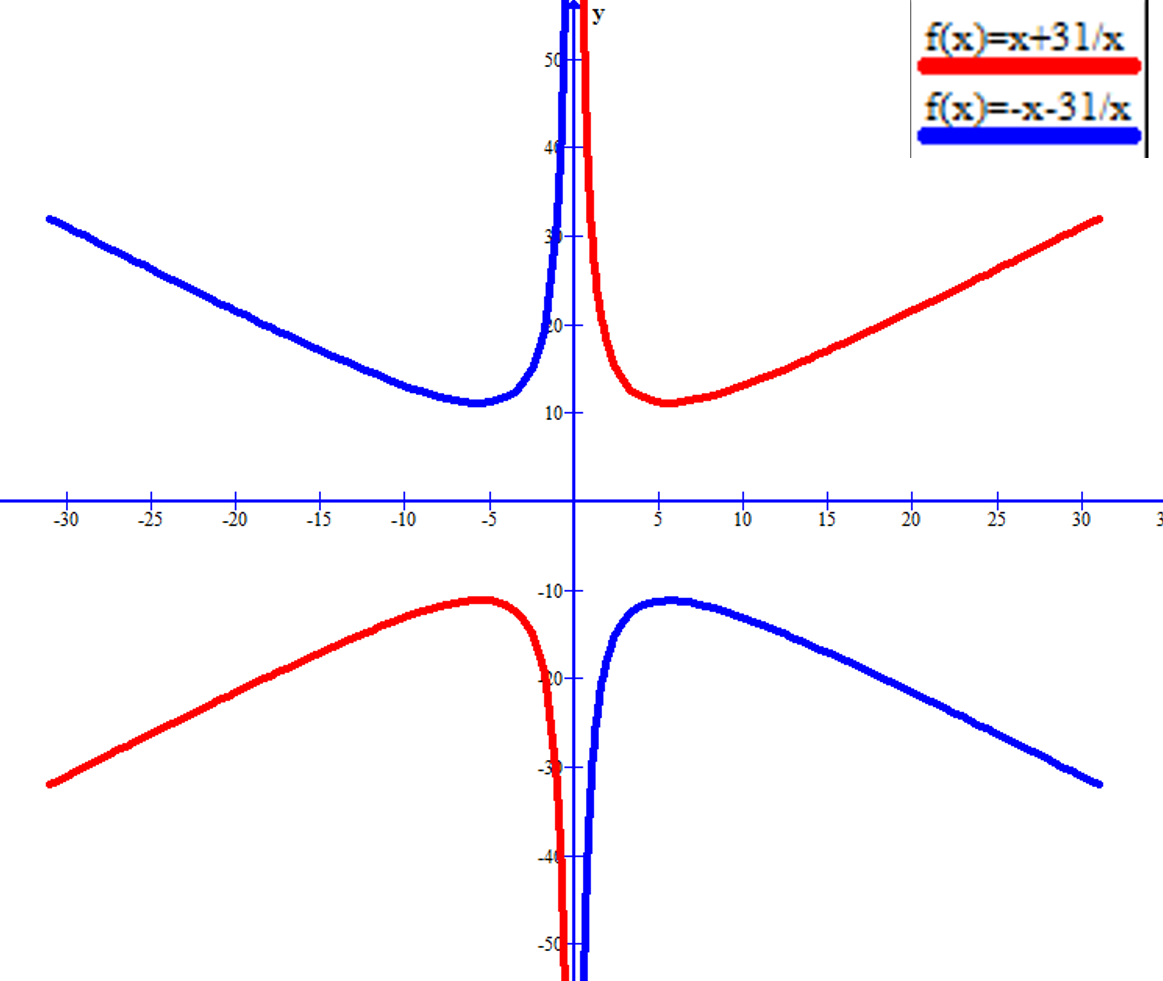 a,c同號的SP函式圖像
a,c同號的SP函式圖像由圖像看出,此類型的SP函式既有反比例函式的雙曲線性質,又有類似於二次函式的圖像特徵。
性質1:圖像與y軸在實數範圍內無交點;
性質2:兩曲線關於(0,b)對稱;
性質3:當a,c分別互為相反數,b相等時,兩函式圖像關於y軸和直線y=b對稱;
性質4:圖像有端點。
(2)a,c 異號:無端點
由圖像看出,此類型SP函式沒有類似二次函式的圖像性質,但仍然有類似反比例函式的雙曲線性。
 a,c異號的SP函式圖像
a,c異號的SP函式圖像性質1:在實數範圍內,圖像與 y 軸無交點。
性質2:當 a,c 分別互為相反數,b相等時,兩函式圖像關於 y 軸和直線 y=b 對稱。
性質3:圖像無端點。
SP函式和對勾函式
當b=0時,SP函式為
,即為高中數學中的對勾函式。此函式又名雙勾函式。
圖像端點和最值的研究
由圖像可知,當 a,c 同號時,SP函式的圖像有端點。那么,端點對應的函式值(即該支函式的最值)與 a,b,c 之間有什麼關係呢?
(1)y=ax+c/x
由於函式圖像的兩支關於原點中心對稱,因此首先以第一象限為研究對象。
∴令
,
。則
在同一平面直角坐標系中作出函式 y1,y2 的圖像,如圖所示。兩函式在第一象限內交於一點P。
 y=ax+c/x 的端點與最值研究
y=ax+c/x 的端點與最值研究∵ y2與 y3相切,
∴在y軸的右側(x>0),不論x取任何值,y1 +y3 恆等於2
,即
。
又由圖可知在 y 軸右側, 當 x ≠
時,y2始終在直線 y3的上方,y2 > y3 ,
∴當
時,
+
有最小值,即
。
 y=ax+c/x:總結
y=ax+c/x:總結同理,在第三象限內,當
時有最大值,
。推理過程和第一象限的基本相同。
y=ax+c/x:總結(如右圖)
(2)y=ax+b+c/x
由於函式圖像的兩支關於(0,b)中心對稱,因此首先以y軸右側的一支為研究對象。
∴令
,
。則
在同一平面直角坐標系中作出函式y1 ,y2 的圖像,如圖所示。兩函式在第一象限內交於一點P。
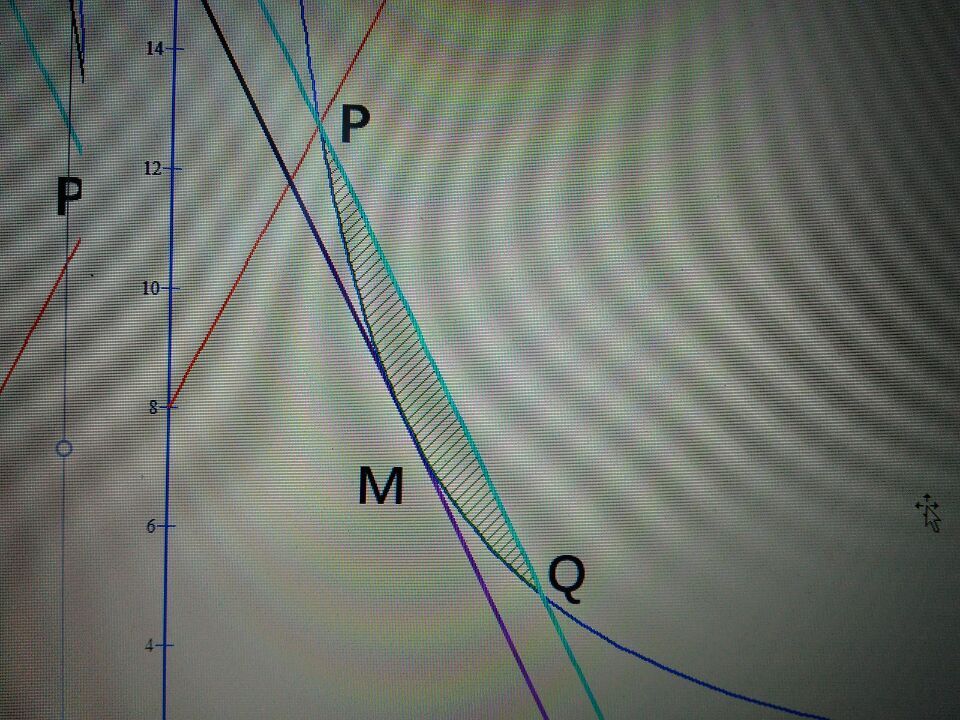 y=ax+b+c/x 的端點與最值研究
y=ax+b+c/x 的端點與最值研究過點P作
,直線 y3與曲線
交於P, Q兩點,則直線y1 ,y3 關於直線
,
對稱。
∵
(1)在 0<x<
和
的範圍內,
在直線
的上方,此時y2>y3, y1+y2>y1+y3;
(2)在
<x<
的範圍內,
在直線
的下方,此時y2‘<y3, y1+y2’<y1+y3,
∴y1+y2'<y1+y3<y1+y2,即y1+y2的最小值的橫坐標在
<x<
的範圍內。
令
,即
,整理得
,
。將
代入
中:
,
,即
。
∴當
時,
+
有最小值,即
。
 y=ax++b+c/x:總結
y=ax++b+c/x:總結同理,在y軸左側,當
時有最大值,
有最大值,
。推理過程和在y軸右側的基本相同。
y=ax+b+c/x:總結(如右圖)
SP函式的擴展研究
(1)概述
SP函式具有強大的擴展功能,可以在原有的
的基礎上添加更高或更低次項。
(2)添加二次項:y=ax^2+bx+c+d/x
添加二次項後的SP函式為:
(2)添加負二次項:y=ax+b+c/x+d/(x^2)
添加負二次項後的SP函式為:
此函式的圖像形似基本SP函式有端點及無端點的兩個圖像的結合。此函式圖像的兩支中,只有一支存在端點,即有最值。該形式SP函式的其他性質與基本SP函式對應性質基本類似。
是SP函式負二次項擴展的最簡單形式,其實質是一次函式 y=ax(a≠0) 與二次函式 y=x^2(x≠0)的反函式y=k/(x^2) 的結合。
SP函式的基本研究已經基本完成,而對於它的擴展研究才剛剛起步。希望“有識之士”能幫助我們修正基本研究中難免存在的問題或缺陷,並不斷完善函式的擴展內容,共同傳承與弘揚“特殊”的精神!
Sp函式、Sp方程與其他數學概念的關係
Sp函式與Sp方程的關係
Sp方程是一元二次方程與分式方程的結合,一般式為
。當Sp函式中y=0時,即為Sp方程的一般形式。Sp方程的解即為Sp函式與x軸的交點。一般的,當a、c同號,b=0時,所對應的Sp方程一般無解。當a、c異號,所對應的Sp方程有兩個不相同的解。
Sp方程與一元二次方程的關係
將Sp方程
兩邊乘以x化為ax
2+bx+c=0(x≠0)即可發現,Sp方程求根公式仍為
。即可得到Sp方程與一元二次方程有必然聯繫。Sp方程的解即為對應一元二次方程的解。


 a, b, c 對SP函式的影響
a, b, c 對SP函式的影響



 a,c同號的SP函式圖像
a,c同號的SP函式圖像 a,c異號的SP函式圖像
a,c異號的SP函式圖像


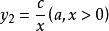

 y=ax+c/x 的端點與最值研究
y=ax+c/x 的端點與最值研究














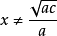





 y=ax+c/x:總結
y=ax+c/x:總結


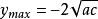


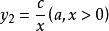

 y=ax+b+c/x 的端點與最值研究
y=ax+b+c/x 的端點與最值研究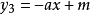

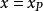
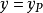



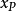


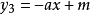
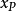


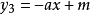
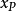

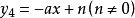








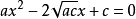





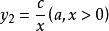
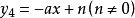





 y=ax++b+c/x:總結
y=ax++b+c/x:總結