基本介紹
- 中文名:函式思想
- 外文名:Theory and thought of function
- 性質:已知+未知+規定思想
- 宗旨:以無限為有限
基本概念,性質,宗旨,數學型問題,形象展現,
基本概念
理論分支: | “和”之《函式思想》 |
英文名稱: | 《Theory and thought of function》 |
性質: | 已知+未知+規定思想 |
宗旨: | 以無限為有限 |
《函式思想》,《“和”的思想》理論體系下的三大理論思想之一。是指用函式的概念和性質去分析問題、轉化問題和解決問題的思維策略。
函式思想體現了:在解決“數學型”問題中的一種思維策略。
具體來說,函式描述了自然界中數量之間的關係,函式思想通過提出問題的數學特徵,建立函式關係型的數學模型,從而進行研究。它體現了“聯繫和變化”的辯證唯物主義觀點。一般地,函式思想是構造函式(即“規定思想”)從而利用函式的性質(已知+未知+規定思想)解題。經常利用的性質是:f(x)、x的單調性、奇偶性、周期性、最大值和最小值、圖像變換等,要求我們熟練掌握的是一次函式、二次函式、冪函式、指數函式、對數函式、三角函式的具體特性。
在解題中,善於挖掘題目中的隱含條件,構造出函式解析式和妙用函式的性質,是套用函式思想的關鍵。對所給的問題觀察、分析、判斷比較深入、充分、全面時,才能產生由此及彼的聯繫,構造出函式原型。另外,方程問題、不等式問題和某些代數問題也可以轉化為與其相關的函式問題,即用函式思想解答非函式問題。
性質
在經過歸納總結後,科學家們用簡潔的一個公式描述了它的性質:“已知+未知+規定思想”。“已知”,就是指“定量”;而“未知”則是指“變數”;至於“規定思想”則是,人們根據事物的規律,人為的構造的一種客觀函式關係去解決問題的一種策略(人為的因素造就一個自我的空間——規定思想)。
宗旨
以無限為有限。
在人類長期運用《函式思想》去解決問題的發展過程中,人們不斷注意到用函式解決問題後都有一個共同特點,或說是一種共同的“指向” ,那便是,它們總是用短小而有限的公式長度去描述一個有著無限數據的事物(變數可以無限的更換,公式就會有無數的值)。
偉大領袖 毛澤東曾說過:“世間的萬事萬物都是本同一類的。”改變世界武術史的偉大的哲學家、武術家、功夫巨擘李小龍也曾這樣描述武術的最高境界:以無法為有法,以無限為有限。
在我讀高中時,一道複雜的數學題使我研究了三天才將其原始答案更加簡潔化,那道題中所描繪的是一個立體圖形,但它卻由一個函式公式表示,並且裡面有兩個變數,並非一般的題型。研究後我發現要想畫出其圖形必須先定義其中一個變數,待畫出其規律圖形後,再使它變回變數然後去定義另一個變數,並畫其規律圖形。結果我發現它是一個DNA雙螺旋結構圖形。為此,我提出了一個大膽的想法:世間的萬事萬物都可以用一個函式公式表達,但要賦予其變數一定的範圍(如果不規定範圍,那么這個事物將會無限的大下去)。倘若有一款神一樣的軟體,那么只要把一塊兒不規則的石頭的函式公式輸入其中,那么軟體便會自動畫出其三維圖形,同時如果不規定其變數的範圍,那么這塊石頭將無法畫出來,因為它變成了無邊無際的。現代科技中,有一些軟體具有類似功能,但還達不到我想像的這么神奇。比如3Dmax、maya等。
數學型問題
所謂“數學型”問題,就是指那些富有數學靈魂的問題。形象地講,譬如化學方程式的配平、有關物理勻變速的計算、管理學的運用等等,它們都是數學類型的問題。客觀的講宇宙間的各種規律變化都離不開“函式思想”。
函式思想滲透於各個領域。用《函式思想》去思考、解決問題,將會大大壓縮、最佳化問題的複雜性。在《函式思想》的傳授和教導中,有著一句俗語:複雜問題簡單化!
形象展現
等差數列和勻變速運動
經典例題1:汽車經過啟動、加速行駛、勻速行駛、減速行駛之後停車,若把這一過程中,汽車的行駛路程S看作時間t的函式,其圖像可能是()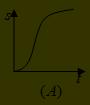 (A)
(A)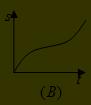 (B)
(B)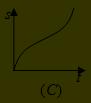 (C)
(C)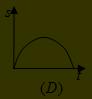 (D)
(D)
 (A)
(A) (B)
(B) (C)
(C) (D)
(D)解:本題考查的是“一階導數的物理意義”。
下面我們將以:“等差數列”和“物理勻加速”→函式→導數的思路來解剖此題,解答此題,並從此基礎上總結出一種簡便的解題“因子”。
第1步、
等差數列:
通項公式:a[n]=a[1]+(n-1)d
前n項和公式:S[n]=(a[1]+a[n])n/2=na[1]+1/2·n(n-1)d
物理勻加速:
末速度:v[t]=v[0]+at
位移:s=1/2·(v[0]+v[t])t=tv[0]+1/2·at^2
第2步、將“等差數列”和“物理勻加速”進行簡化,變成函式式。
等差數列:
通項公式:a[n]=dn+b(其中,d為公差,b=a[1]-d)
前n項和公式:S[n]=An^2+Bn(其中,A=d/2,B=a[1]-d/2)
【即公式中“b、A、B”都是定量,而n是變數(注意:[]符號裡面的字元為定量右下角的標籤),顯而易見:a[n]為“一元一次函式”;S[n]為“一元二次函式”】
物理勻加速:(同理)
末速度:v[t]=at+v[0](加速度a和初速度v[0]為定量)
位移:s=a/2·t^2+v[0]t
綜合第1、2步克的結論:“物理勻加速公式”屬於“等差數列”。
【備註:由公式可看出
1、{a[n]}是一條直線,必過(1,a[1])點,且斜率k=d(公差);
2、{S[n]}是二次方程(Quadratic Equation)圖像,必過(0,0)點和(1,a[1])點;
3、S[n]的導數(S[n])`與相應的{a[n]}直線的斜率相等,且a[n]的圖像等於(S[n])`切線向下移動d/2個單位】
第三步、導數:
因為,位移s公式是一元二次函式
所以, s的“一階導數”s`=(a/2·t^2+v[0]t)`=at+v[0]=v[t];
s的“二階導數”s``=v`[t]=(at+v[0])`=a.
所以,s的“一階導數”表示“速度”,“二階導數”表示“加速度”。
因此,本題考點技巧為:
即A→B斜率k↓,推理出v↓,所以為“減速運動”;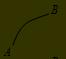 凸
凸
 凸
凸即A→B斜率k↑,推理出v↑,所以為“加速運動”; 凹
凹
 凹
凹即A→B斜率k不變,推理出v不變,所以為“勻速運動”。 直
直
 直
直所以,只要把以上“三步”壓縮成一個模版,變成一種“知識因子”存入大腦,那么解答此題時,耗時將不會超過一秒。
拓展思維等比數列
通項公式:a[n]=a[1]q^(n-1)=cq^n【c=a[1]/q】
前n項和公式:S[n]=a[1](1-q^n)/(1-q)【q≠1】
總結:
1、{a[n]}為“指數函式”,且圖像必過(0,a[1]/q)點和(1,a[1])點;
2、單調性:
{a[n]}為增函式,互推a[1]>0,q>1或a[1]<0,0<q<1;
{a[n]}為減函式,互推a[1]<0,q>1或a[1]>0,0<q<1;
{a[n]}為常函式,互推q=1;
{a[n]}為擺動數列,互推q<0.
化學方程式配平
經典例題2: a.離子方程式
_NH4″+_O2→_NO3′+H″+_H2O【″為正離子,′為負離子】
解:Ⅰ、分別設NH4″、O2為x、y,則由物量守恆得:
x NH4″+ y O2→ x NO3′+ (10x-4y) H″+ (2y-3x) H2O
Ⅱ、由電荷守恆得:
x=(-x)+(10x-4y)=9x-4y → 2x=y
取最小倍數即得:x=1,y=2
b.分子方程式
Cu2S與一定濃度的HNO3反應,生成Cu(NO3)2、CuSO4、NO2、NO和H2O,當NO2和NO的物質的量之比為1:1時,實際參加反應的Cu2S與HNO3的物質的量之比為()
A.1:7; B.1:9; C.1:5; D.2:9
解:列出題中所述反應方程式,並設Cu2S、HNO3分別為x、y,n(NO2):n(NO)=p:p
則,x Cu2S + y HNO3= x Cu(NO3)2+ x CuSO4+ p NO2+ p NO + y/2 H2O
得物量守恆:
N守恆:y=2x+2p
O守恆:3y=6x+4x+3p+y/2
合併兩式,同時消去p得:x/y=1/7.所以,選A.
用《函式思想》去解決化學方程式配平的問題,將會更精準、迅速,且易學。
愛因斯坦的相對論
時間、長度、質量的關係 計算Δt、l、m時,“(1-(v/c)²)½”做為一個函式因子代入,即設(1-(v/c)²)½”=μ。
則Δt=Δt`/μ、l=l`μ、 m=m1/Δt(其中,Δt、Δt`分別為靜止時的時間變化、相對運動時的時間變化;l、l`分別為靜止者看到的運動物長度、相對靜止時物體的長度;m、m1分別為運動物的質量、物體相對靜止時的質量)
這裡巧妙、靈活的運用了《函式思想》,引入了“函式因子”這一概念,使其形成了一種函式模版。這使得一些複雜的式子得以明了、清晰化。
經典的運用
經典例題3:這裡主要是鞏固“經典例題1”中所學到的知識,以進一步加強對《函式思想》的理解。
“神舟”六號飛船完成了預定空間科學和技術試驗任務後,返回艙於2005年10月17日4時11分開始從太空向地球表面按預定軌道返回,在離地10km的高度打開阻力降落傘減速下降,這一過程中若返回艙所受阻力與速度的平方成正比,比例係數(空氣阻力係數)為k,設返回艙總質量M=3000kg,所受空氣浮力恆定不變,且認為豎直降落。從某時刻開始計時,返回艙的運動v=t圖像如圖中的AD曲線所示,圖中AB是曲線在A點的切線,切線交於橫軸一點B,坐標為(8,0),CD是平行橫軸的直線,交縱軸於C點,坐標為(0,8)。g取10m/s²,請解決下列問題: 經典例題3
經典例題3
 經典例題3
經典例題3〈1〉在初始時刻v1=160m/s時,它的加速度多大?
〈2〉推證空氣阻力係數k的表達式並算出其數值。
〈3〉返回艙在距離高度h=1m時,飛船底部的4個反推力小火箭點火工作,使其速度由8m/s迅速減至1m/s後落在地面上,若忽略燃料質量的減少對返回艙總質量的影響,並忽略此階段速度變化而引起空氣阻力的變化,試估算每支小火箭的平均推力(計算結果取兩位有效數字)。
函式思想無處不用
為了使讀者放開思維去徹底的了解《函式思想》,以下我們將舉一個生活中最常見的例子,來說明《函式思想》運用的廣泛性,同時也要讓大家感受到和明白《函式思想》無處不被用到。
很多騰訊用戶和銀行客戶在設定QQ密碼和帳號密碼時遇到同樣的難題。這樣的現象尤為體現在擁有多個帳號的客戶。就拿QQ用戶來說吧,假設一個boy有五個或是更多的QQ帳號,在他設定密碼時,為了提高安全性,他不想設定成一樣的密碼,這個問題該怎么解決呢?
這裡,如果你擁有了《“和”的思想》,在思想上有了很高的覺悟,做事有策略性、寫文章有明確的條理性,是一個會看書的人,那么你就可以利用《函式思想》輕鬆的解決這個問題了。
1、首先,你要自己確立個(或構造個)函式密碼公式。如“521zuguoandX”(寓意:我愛你,祖國,還有X),在這裡,“521zuguoand”是定量,“X”是變數,你構造這個函式的過程是一個“規定”的過程(即你首先要有這種主動去“構造”、去“規定”的意識,這是一種“規定思想”)。
2、然後你就可以運用了,譬如:你的第一個賬號密碼是“521zuguoandmama(我愛你,祖國我的媽媽)”;第二個帳號密碼則可以改為“521zuguoanddahai(我愛你,祖國我的)”……也就是說,你可以在自己構造的函式公式里任意定向改變變數,是其對應一個或多個帳號。

